The Compilers’ Front End

Regex -> NFA -> (Min) DFA

Regex describes a language

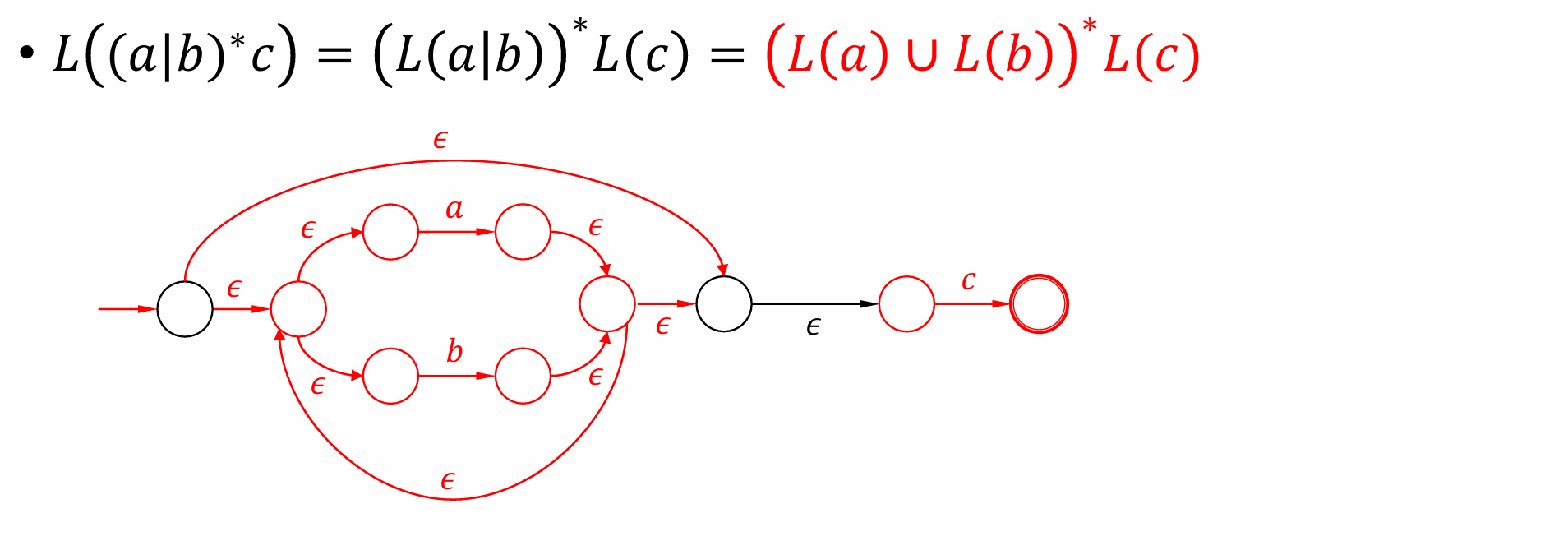
Example: $ (𝑎|𝑏)^∗c$

Given two regex: $r_1,r_2$, the following are regex:

  1. $𝐿(𝑟_1 | 𝑟_2) =𝐿(𝑟_1)∪𝐿(𝑟_2)$
  2. $𝐿(r_1r_2) =𝐿(𝑟_1)𝐿(𝑟_2)$
  3. $𝐿(𝑟_1^∗) = (𝐿(𝑟_1))^∗$
  4. $𝐿((𝑟_1)) = 𝐿(𝑟_1)$

Primitive regex

image-20250618095230189

⭐Build the NFA for the regex

Rules

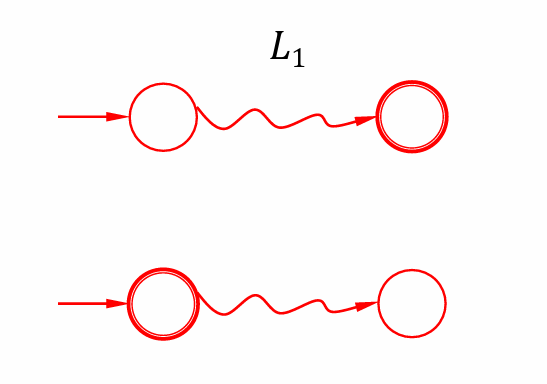
  1. $L_1 ∪ L_2$

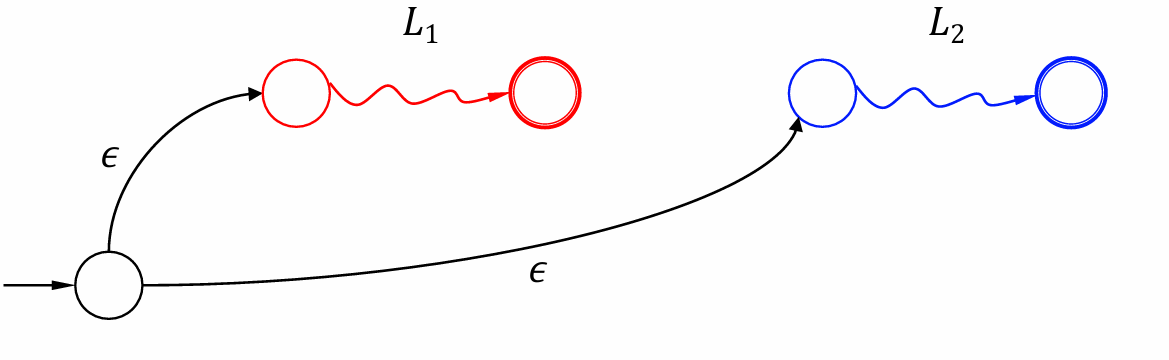
    ​ image-20250618101108287

  2. $L_1L_2$

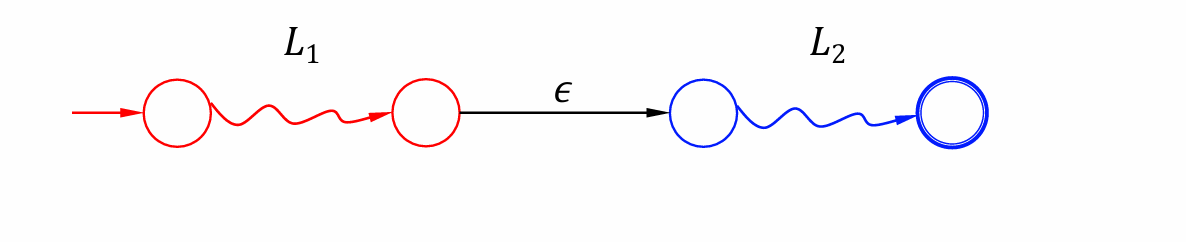
    ​ image-20250618101134835

  3. $L_1^R$

    ​ image-20250618101203899

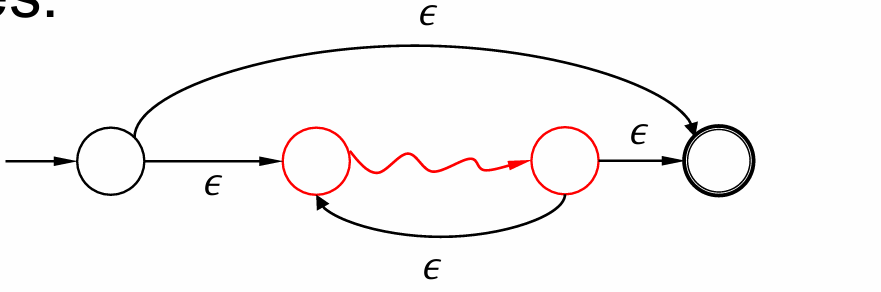
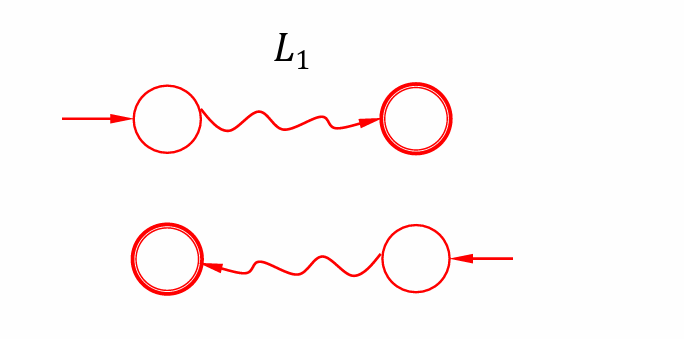
  4. $L_1^*$

    ​ image-20250618101242546

  5. $\overline{L_1}$

    ​ img

  6. $L_1 \cap L_2 = \overline{\overline{L_1} \cup \overline{L_2}}$

Laws

​ img

​ img

​ img

​ img

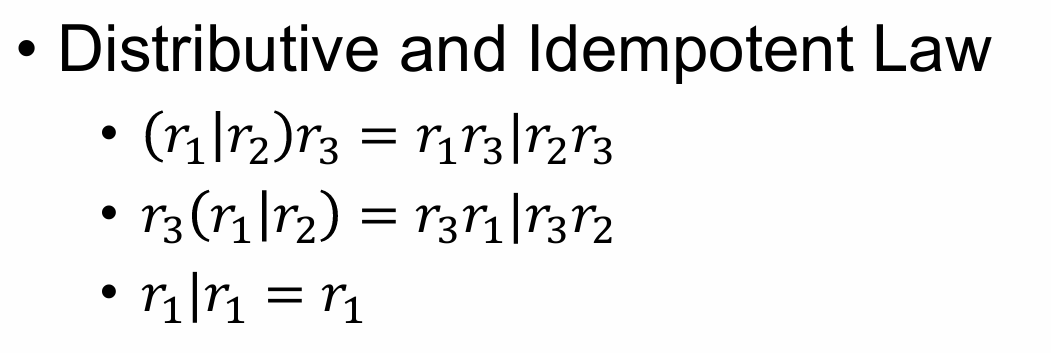
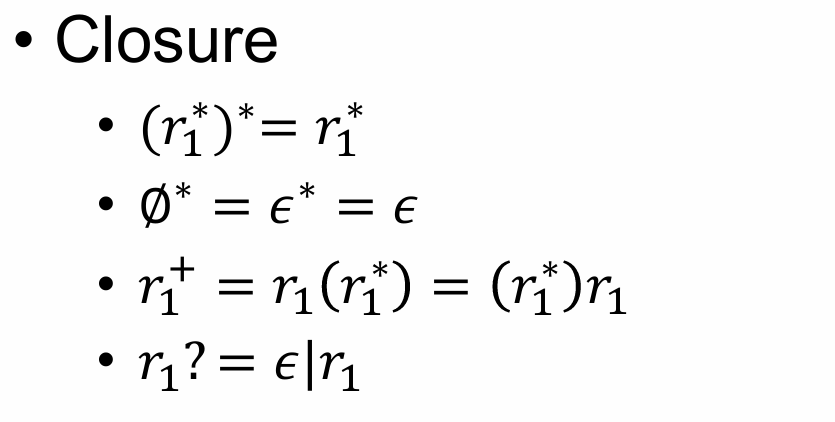
Example

$(𝑎|𝑏)^∗c$

​ image-20250618095557414

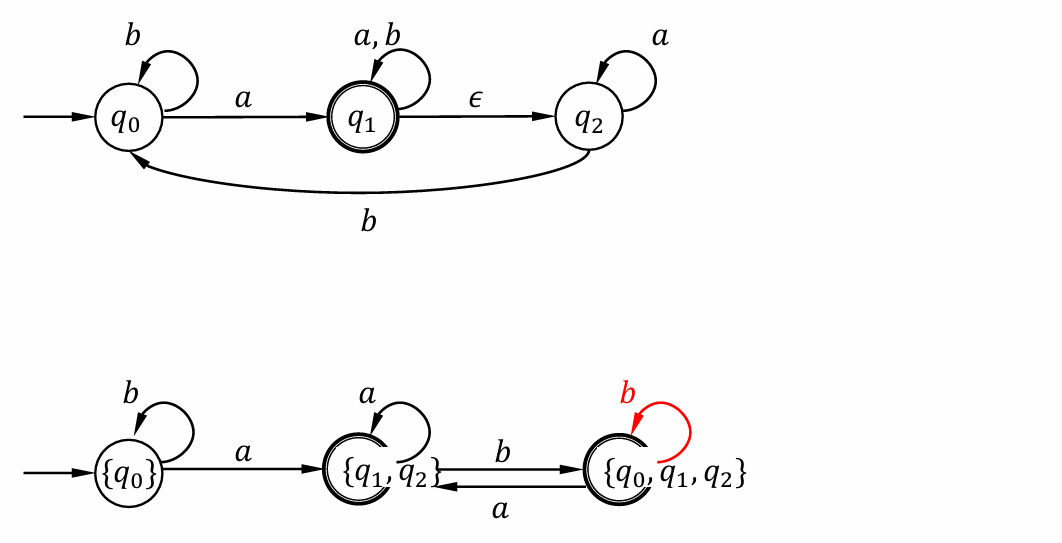
⭐From NFA to DFA

A subset of NFA states is a DFA state

Steps: Subset Construction

ε-closure：指当前状态以及当前状态通过一次或多次ε转移可以到达的状态的集合

  1. 初始ε闭包为$Q_0$
  2. 对于$Q_i$，求其经过某输入符号(比如说x)后可达的状态集合(包括这些状态的ε闭包的元素)为$Q_{i+1}$
  3. 构造路径 $Q_i \overset{x}{\rightarrow} Q_{i+1}$
  4. 如果某个Q包含终结状态，Q也设为终结状态
  5. 重复过程2，3

image-20250618103731621

Example

​ image-20250618102544960

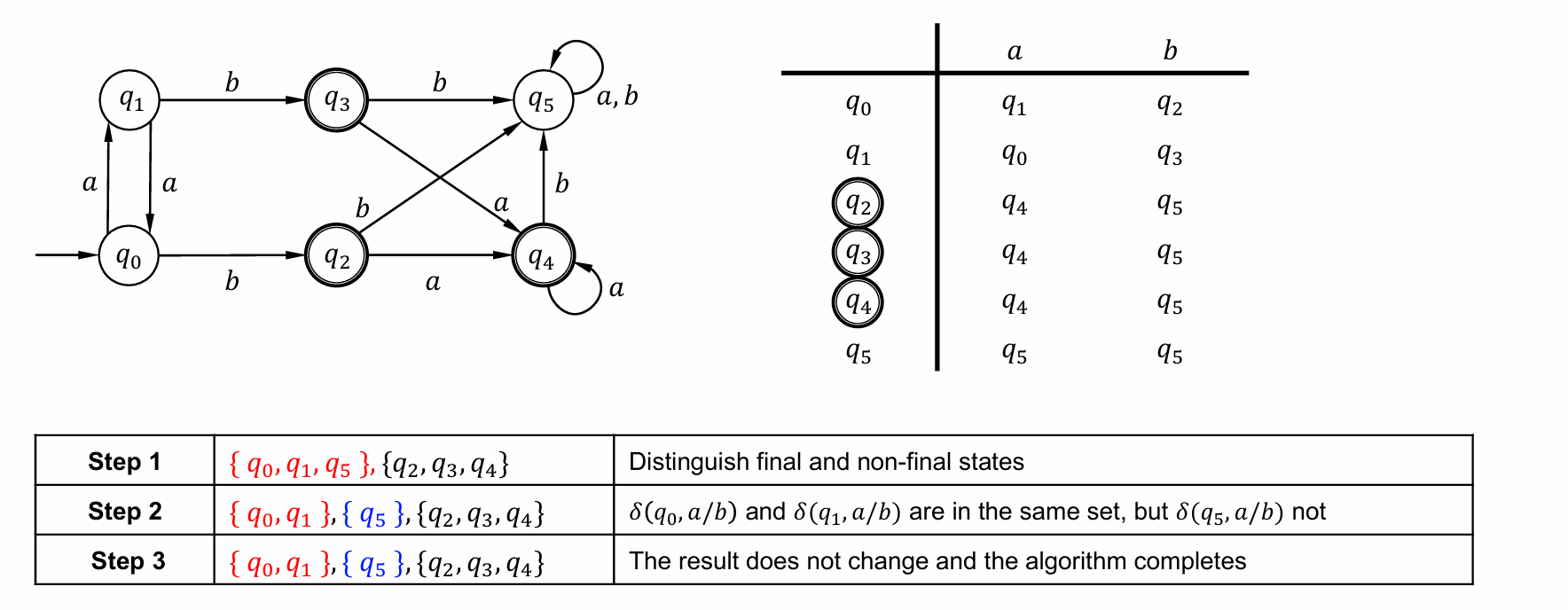
⭐DFA Minimization

Steps

  1. 把终结状态集和非终结状态集分开，分别考察是否可以再区分
  2. 对于任意一个状态集合，考察他们对于同一输入的结果是否在同一集合内，是，则不用再区分；否，根据不同结果区分；
  3. 重复过程2直到没有集合可以再区分

Example

image-20250618104937241

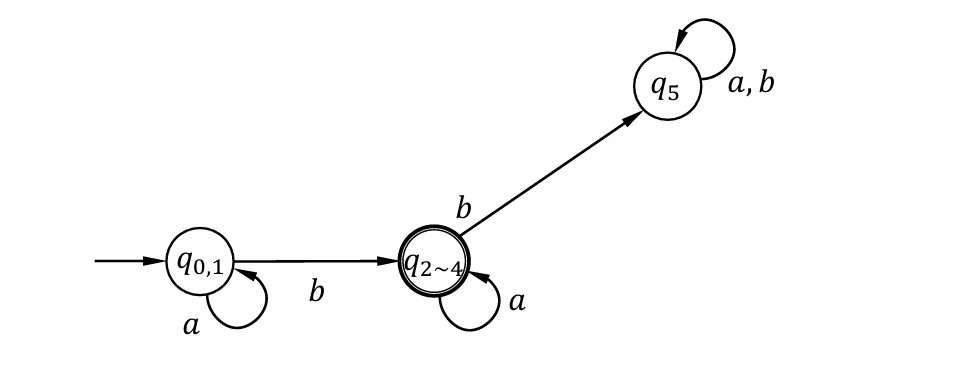
​ image-20250618105446959

DFA to Regex

​ image-20250618110011890

CFG and Parsing

A context-free grammar is a tuple 𝐺 = (𝑁,𝑇,𝑆,𝑃)

​ img

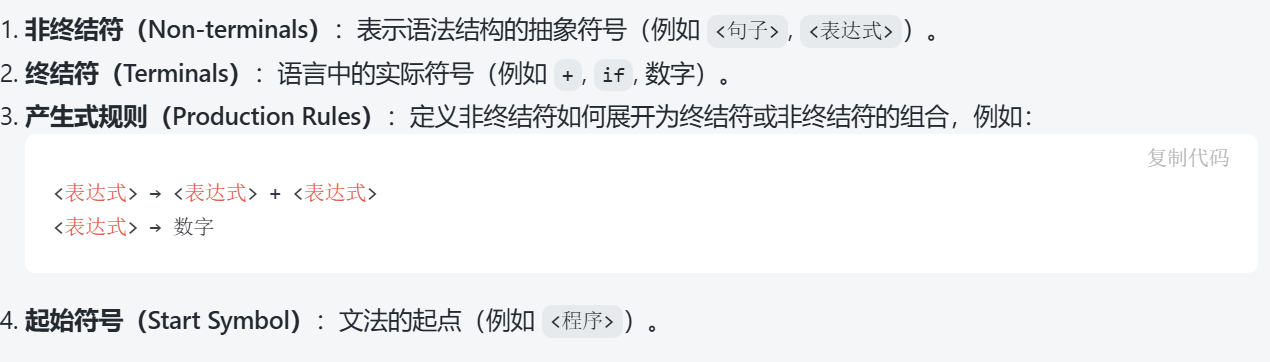
⭐Context Free Grammar (CFG)

From Regex to CFG

  1. $0*1*$

    S -> A B
A -> ε | A 0
B -> ε | B 1

  2. $0n1n$

    S -> 0 S 1 | ε

  3. $0n1{2n}$

    S -> 0 S 11 | ε

  4. $𝑎i𝑏j𝑐^k$ where i = j or j = k

    S -> M N | P Q
M -> a M b | ε
N -> N c | ε
P -> P a | ε
Q -> b Q c | ε

⭐Eliminating Left-Recursion

Non-terminal A that $A \Rightarrow^+ A \alpha$

立即左递归，形如：$$A \rightarrow A \alpha | \beta$$，可以改写为：

$$A \rightarrow \beta A’ \ A’ \rightarrow \alpha A’ | \epsilon$$

一般的（注意$\epsilon$），

​ img

间接左递归，经过多次推导得到$A\alpha |\beta$

img

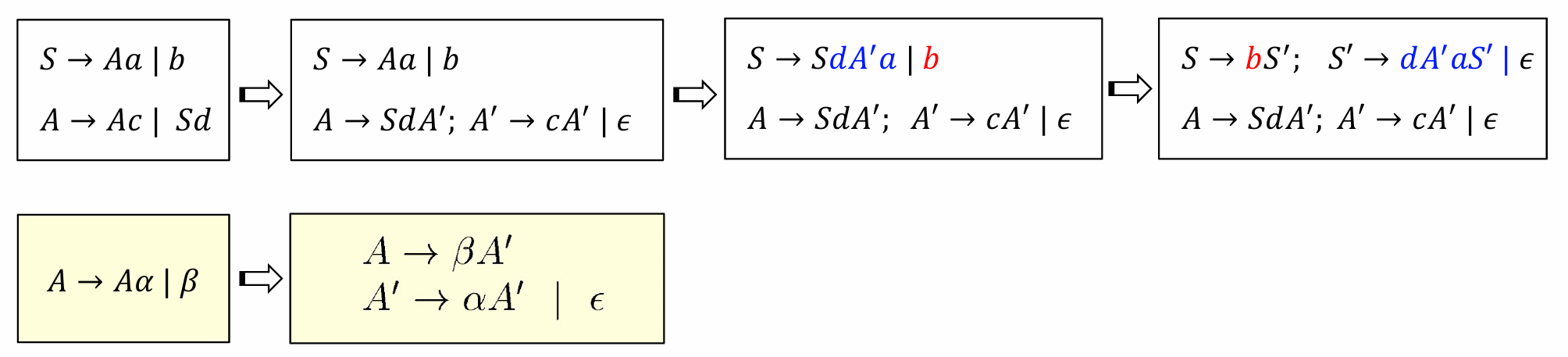
一定不要忘了$\epsilon$，对于间接左递归，先处理可以直接处理的，然后推导至没有左递归为止

⭐LL(1)

LL(1)的含义为：第一个L表明自顶向下分析时从左向右扫描输入串，第二个L表明分析过程将最左推导，1表明只需向右看一个符号便可决定如何推导，即选择那个产生式进行推导。说的是编译器从你写的代码中的每行的左边开始读取字符，到右边结束进行下一行读取；分析也是从每行代码的左边字符开始，到右边结束进行下一行；1表示一种状态接受输入时能唯一的确定下面的状态。

LL(1) rules

一个文法是 LL(1) 的当且仅当：

  1. 不含 左递归
  2. 对每个非终结符 A 和任意两条产生式 A → α | β，满足：FIRST(α)∩FIRST(β)=∅
  3. 若 ε ∈ FIRST(α)，则必须满足：FIRST(β)∩FOLLOW(A)=∅

parsing table

FIRSIT() 开始符号集
就是找括号里第一个字符的终结字符集，如下面找A的开始字符集，显而易见，它的两个非终结字符如下图。

​ img

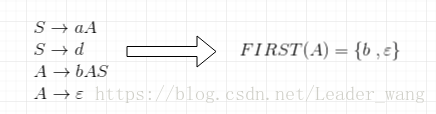
FOLLOW()后跟符号集
同理，寻找括号内后边紧跟的终结字符集，下图跟在A后面的S为非空终结符，但我们要的是终结符，对S求FIRST得到a和d；还有一个后面什么也没跟，那就是$，综上就可以得到下面的答案。

​ 在这里插入图片描述

课件里说的是$，最好按课件来

FIRST()在内部，FOLLOW()在外部

image-20250618140741919

在上例中:

非终结符 FIRST集 FOLLOW集
E {(, id} {), $}
E' {+, ε} {), $}
T {(, id} {+, ), $}
T' {*, ε} {+, ), $}
F {(, id} {*, +, ), $}

  1. 对于FIRST(α)中的每个终结符a，将A→α加入到M[A, a]中

  2. 如果FIRST(α)中有ε，即可能推导出空，就找FOLLOW集对应的位置填A→α

    比如这里有 E'->ε，而FOLLOW(E')={), $}，那么就在M[E’,)]和M[E’,$]的地方写E'->ε

IR Generation

Three-Address Code

​ image-20250618142710982

四元式法：

​ img

Static Single-Assignment

• Feature 1: Every variable has only one definition

• Feature 2: Using φ to merge definitions from multi paths

​ image-20250618142755045

​ img

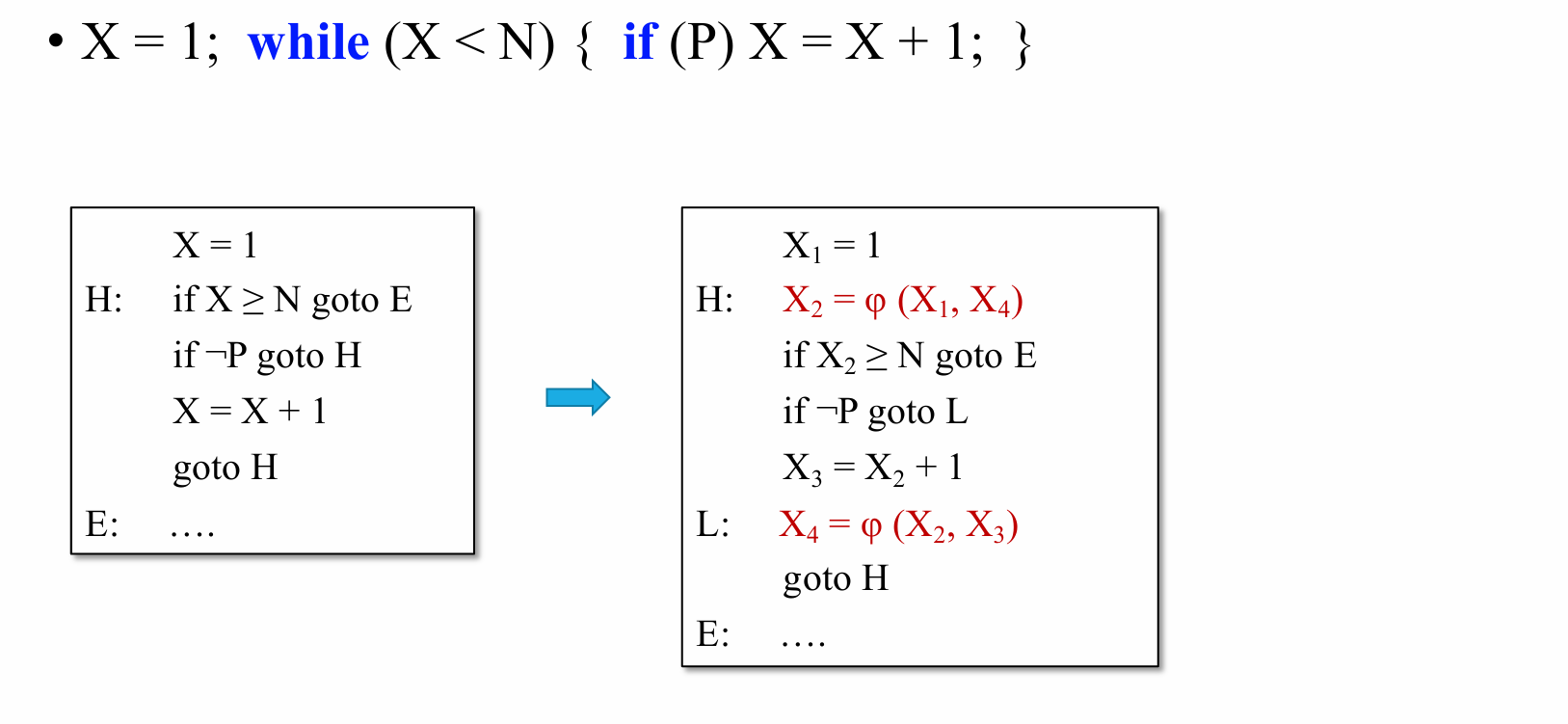
⭐Dominance Relations

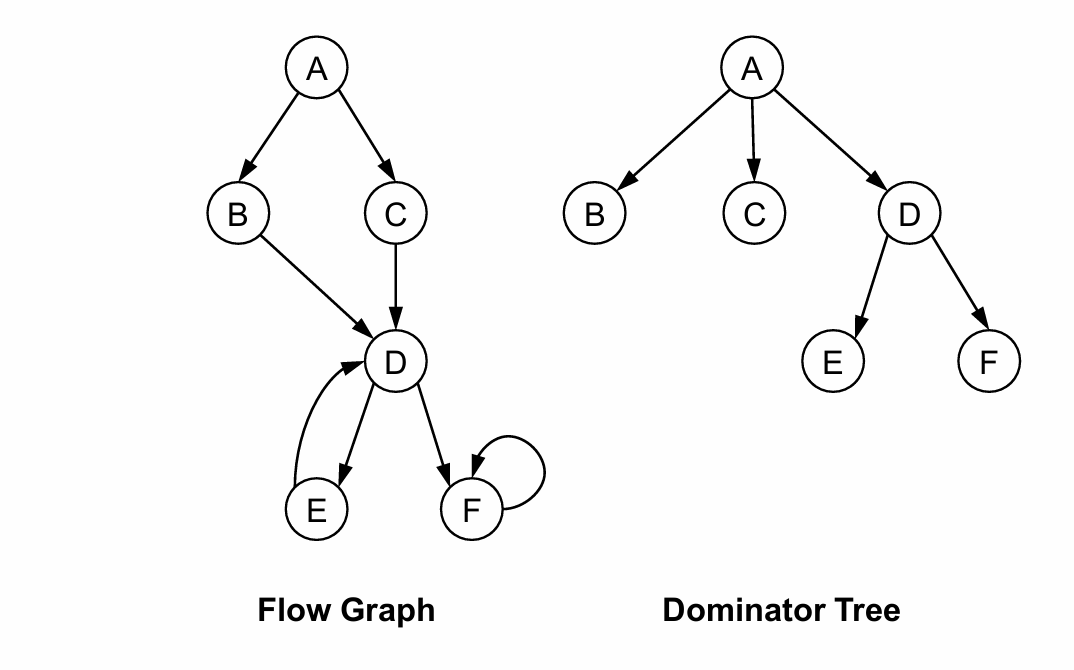
• A dom B

  • if all paths from Entry to B goes through A

• A post-dom B

  • if all paths from B to Exit goes through A

严格支配（被支配）：A (post-)dom B but A ≠ B

直接支配 A strict-dom B, but there’s no C, such that A strict-dom C, C strict-dom B

Dominator Tree

​ image-20250618143030958

Dominance Frontier

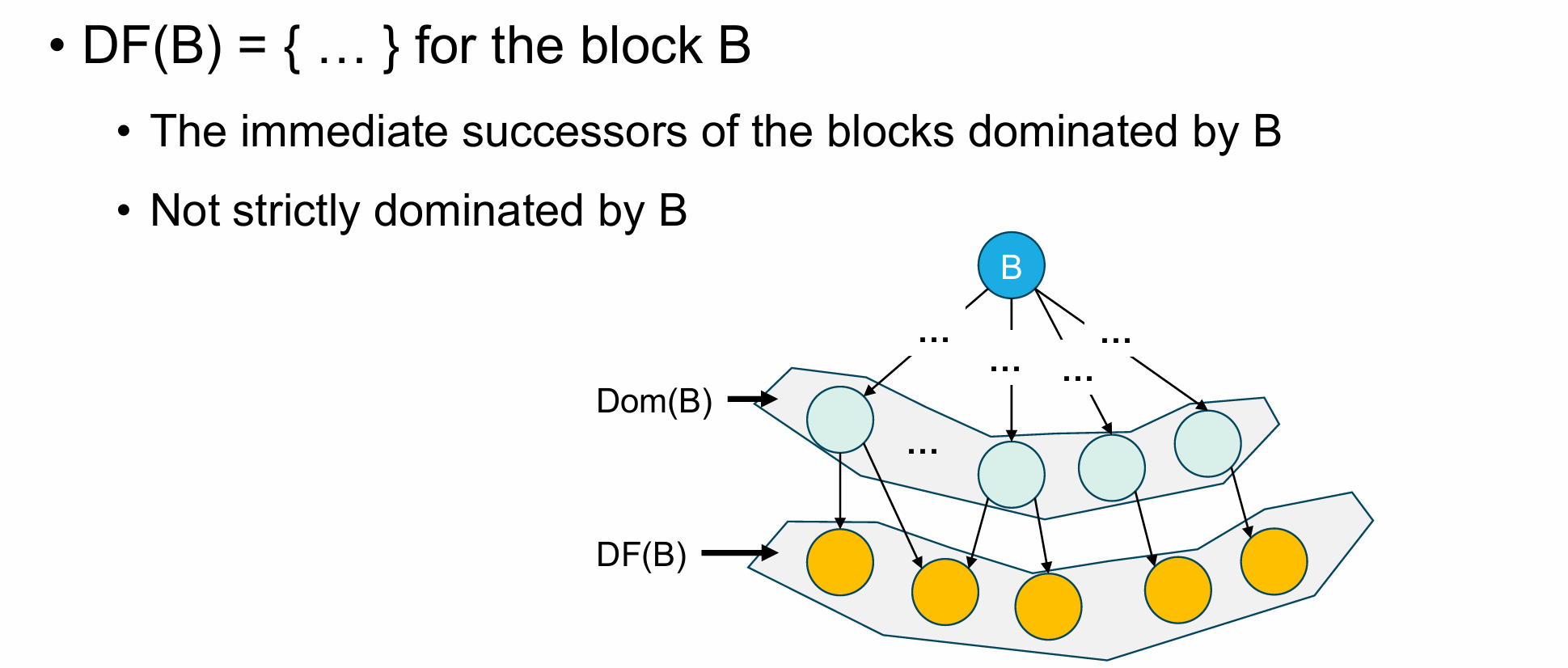
​ image-20250618143116345

​ img

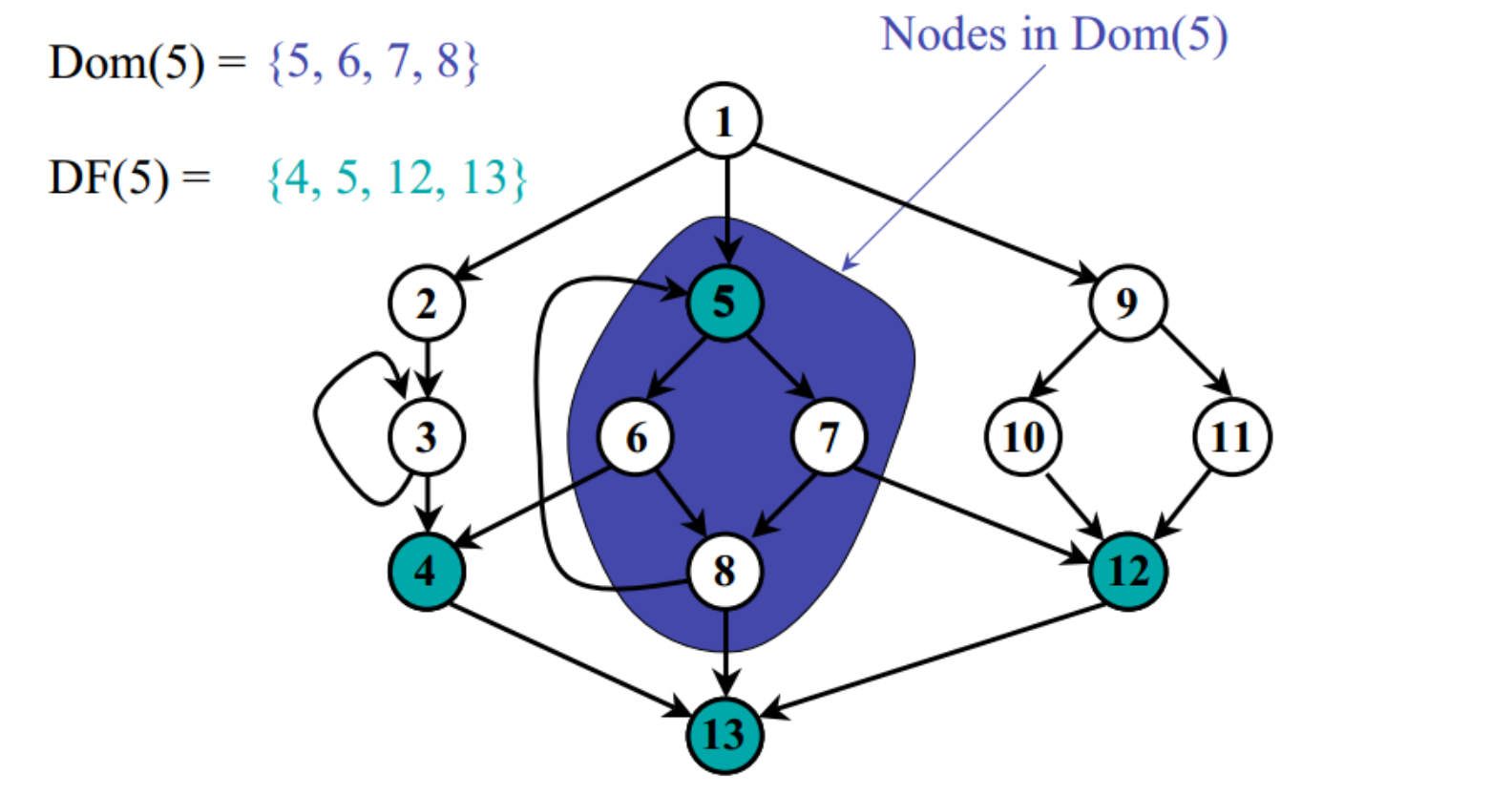
支配边界，顾名思义就是支配区域的边界，这个边界本身不属于被支配的部分

Iterated Dominance Frontier

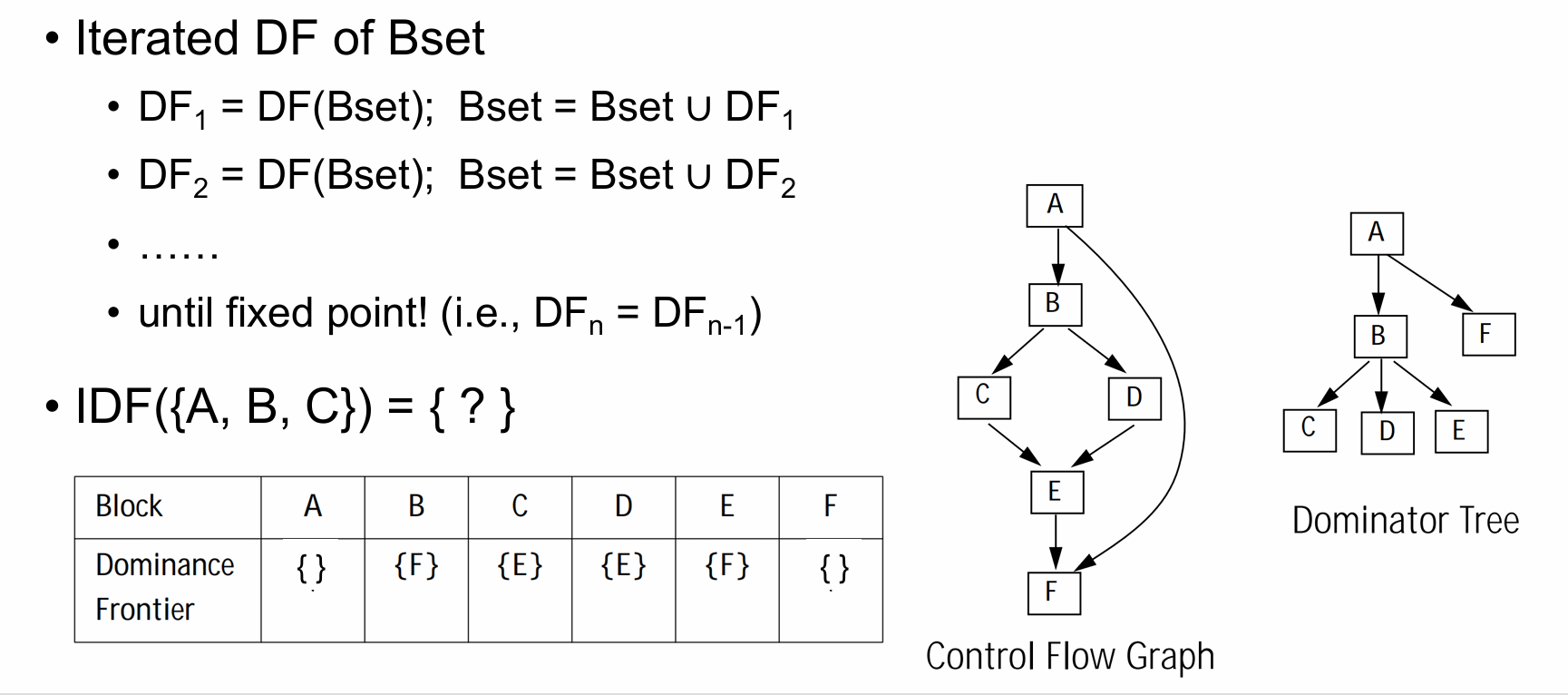
​ image-20250618144848972

IDF({A,B,C})={E,F}

The Compilers’ Middle End

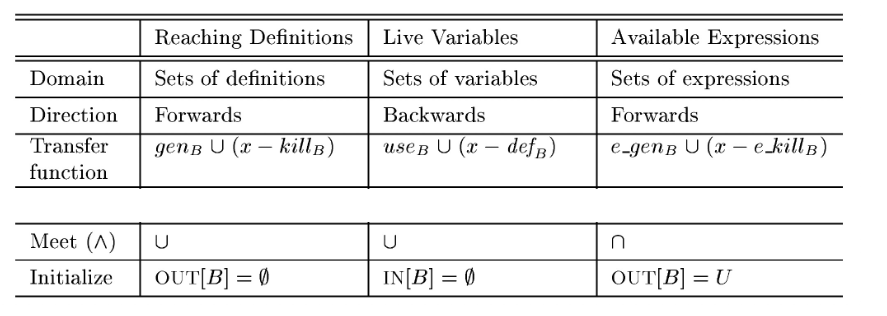
⭐Data Flow Analysis

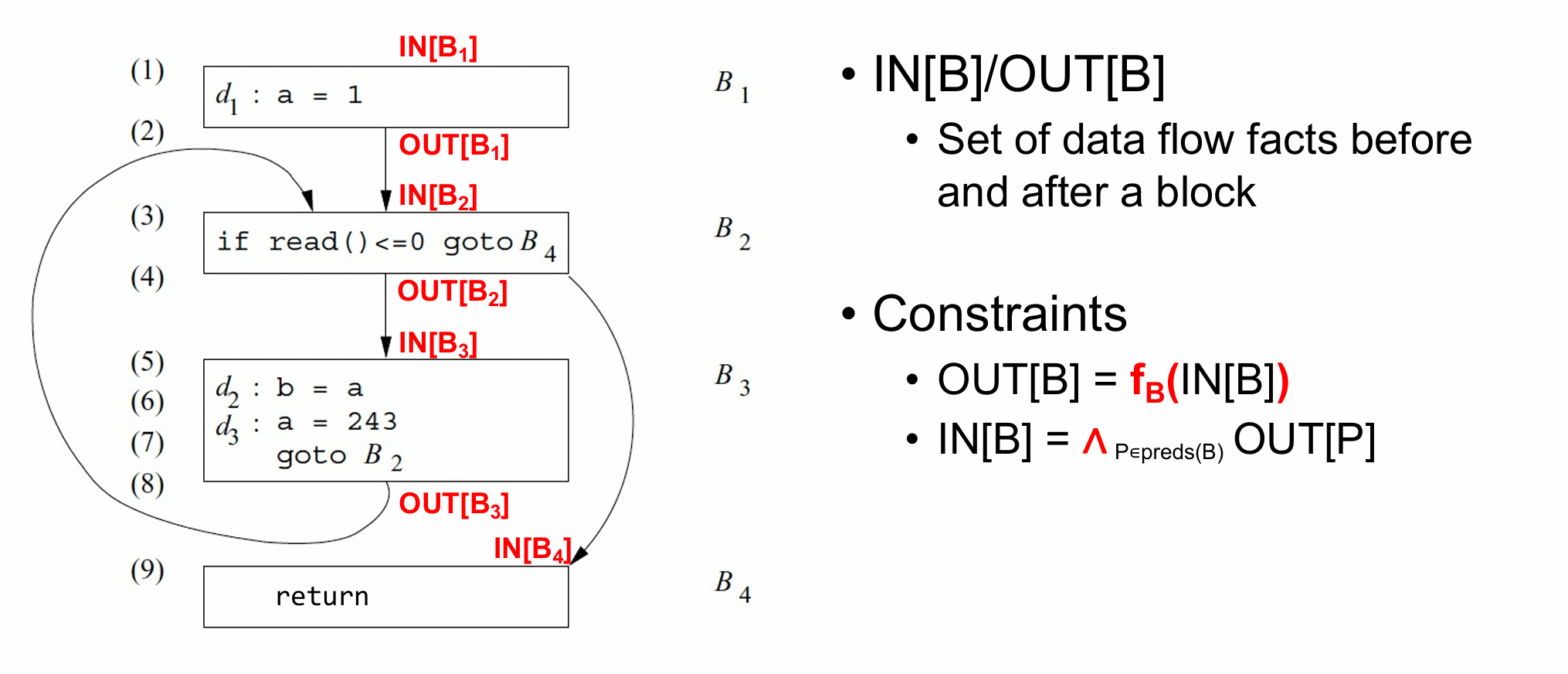
​ image-20250618145128887

To perform data flow analysis, define

  • transfer function $f$ for each statement/block
  • merge function $∧$ at the joint point of multiple paths
  • the initial set of data flow facts for each block

Data flow analysis produces

  • IN[B]/OUT[B] that include data flow facts at a program point
  • The resulting data flow facts are always true during program execution

The Worklist Algorithm

ForEach 
	basic block B: initialize IN[B] and OUT[B]; 
EndFor
worklist = set of all basic blocks;

While (!worklist.empty()) Do;
	B = worklist.pop();
	IN[B] = ∧P∊preds(B) OUT[P];   
	OUT[B] = fB(IN[B]);
	If OUT[B] changed: 
		worklist.push(all B’s successors); 
	EndIf
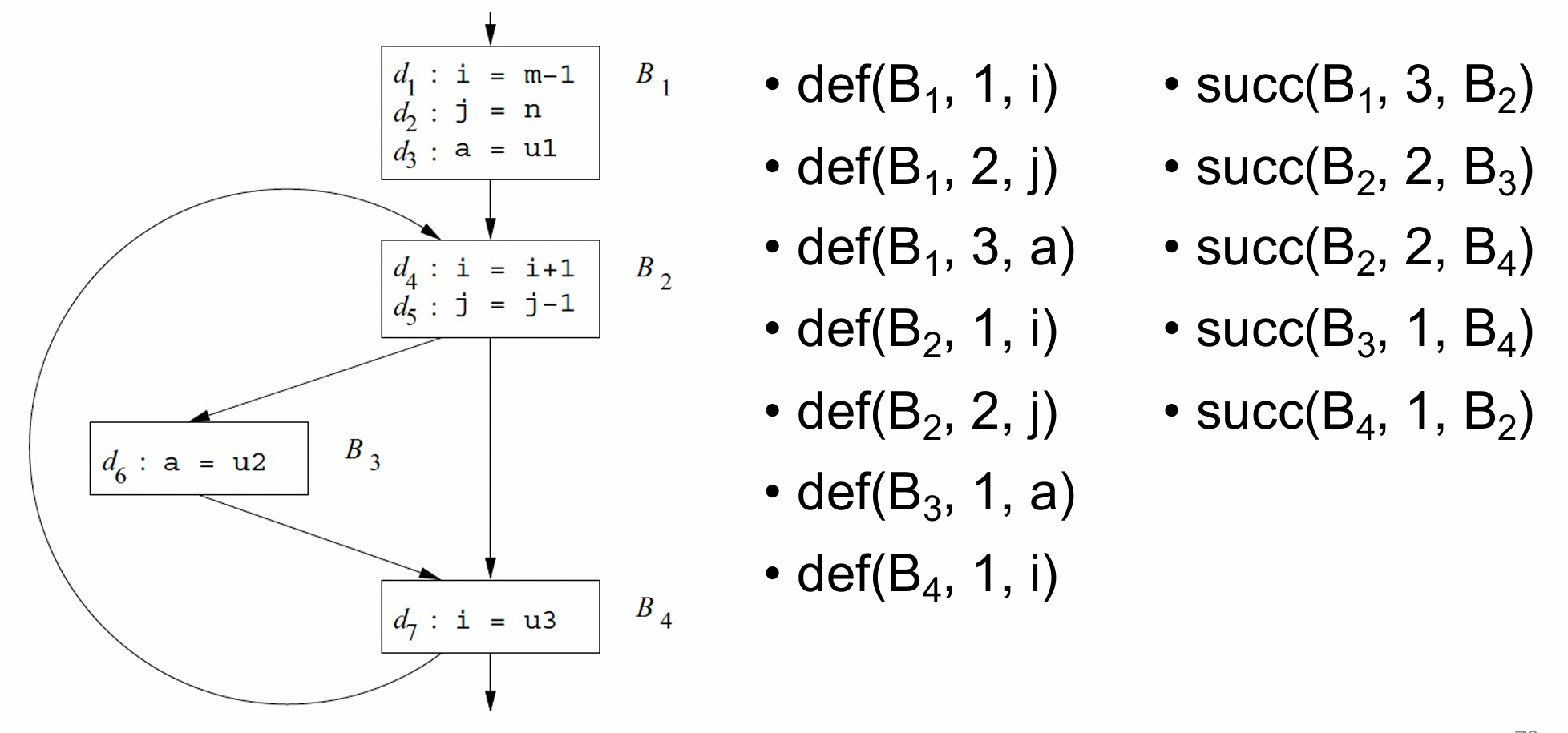
EndWhile

Reaching Definition

​ img

​ img

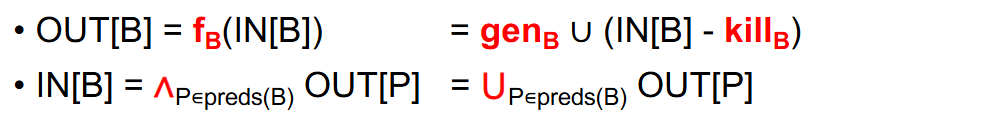
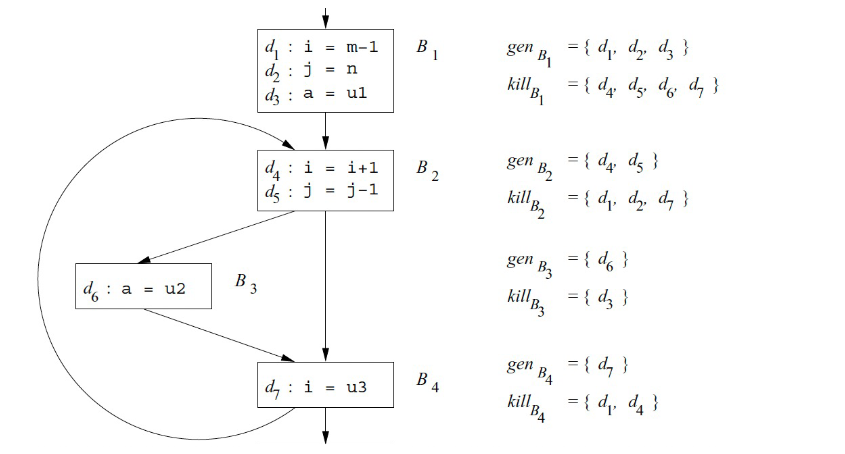
gen是指新定义，包含定义新变量和旧变量重新赋值

kill是指旧定义被覆盖

B4中，d7是gen，而之前的d1，d4就被kill了（d1，d4都是对i的赋值）

Available Expressions

在程序点 p 处，表达式 e 是可用的，当且仅当：

  1. 已计算：从程序入口到 p 的所有路径上，e 均已被计算过。
  2. 未被修改：所有路径上 e 的操作数（变量）在最后一次计算 e 后未被重新定义。

​ img

​ img

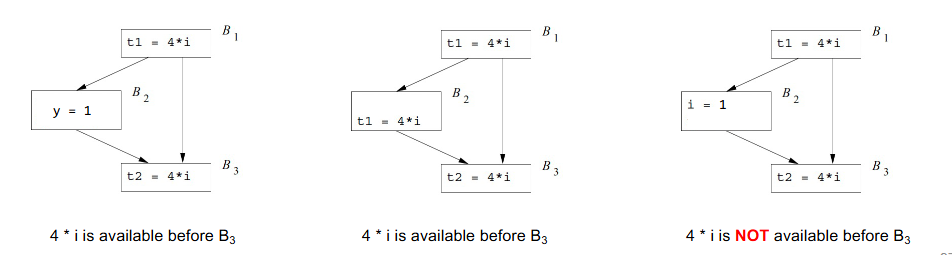
c=b+c ，c的值发生了变化

Live Variables

点 p 处的变量 x 的值是否可以沿从 p 开始的路径上继续使用

Summary

img

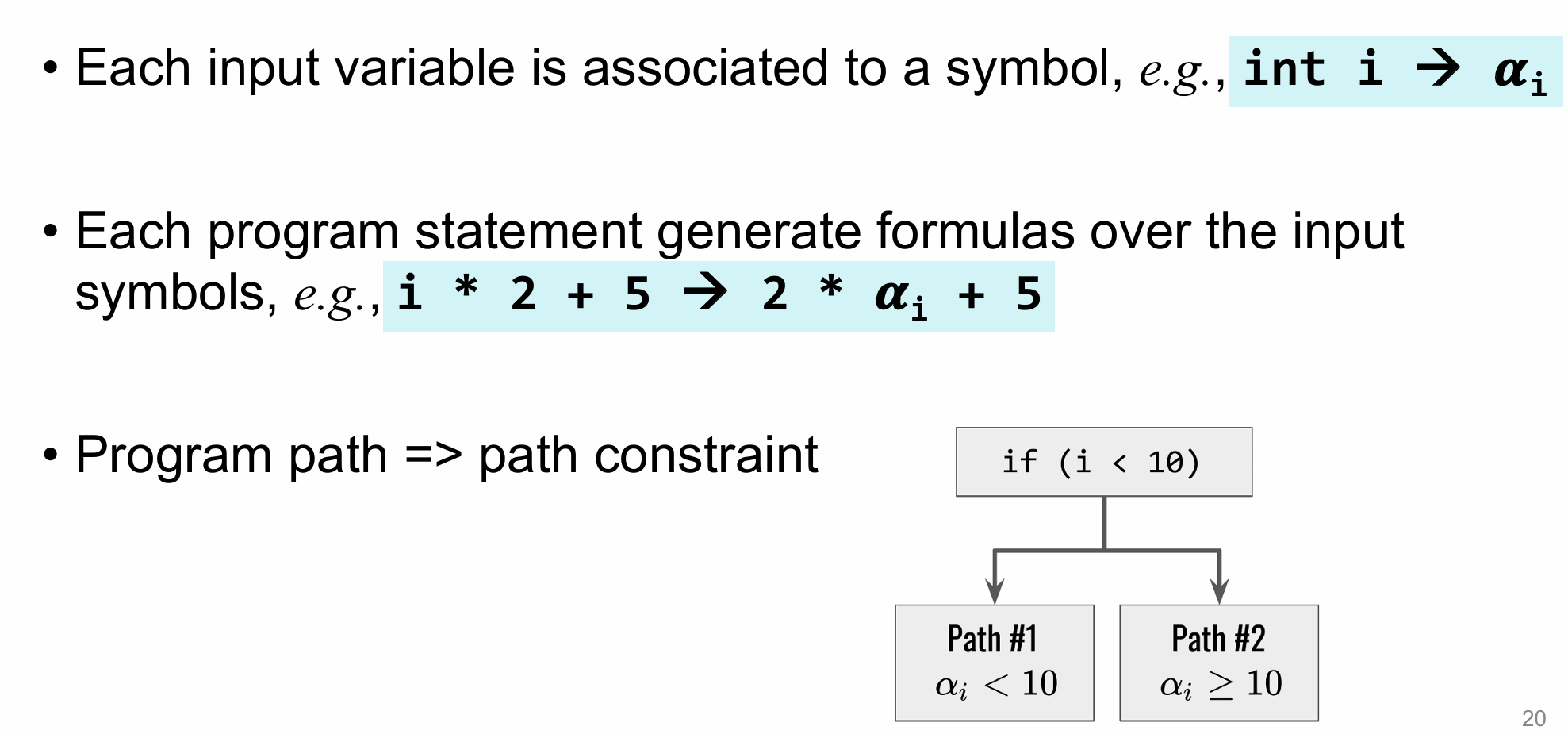
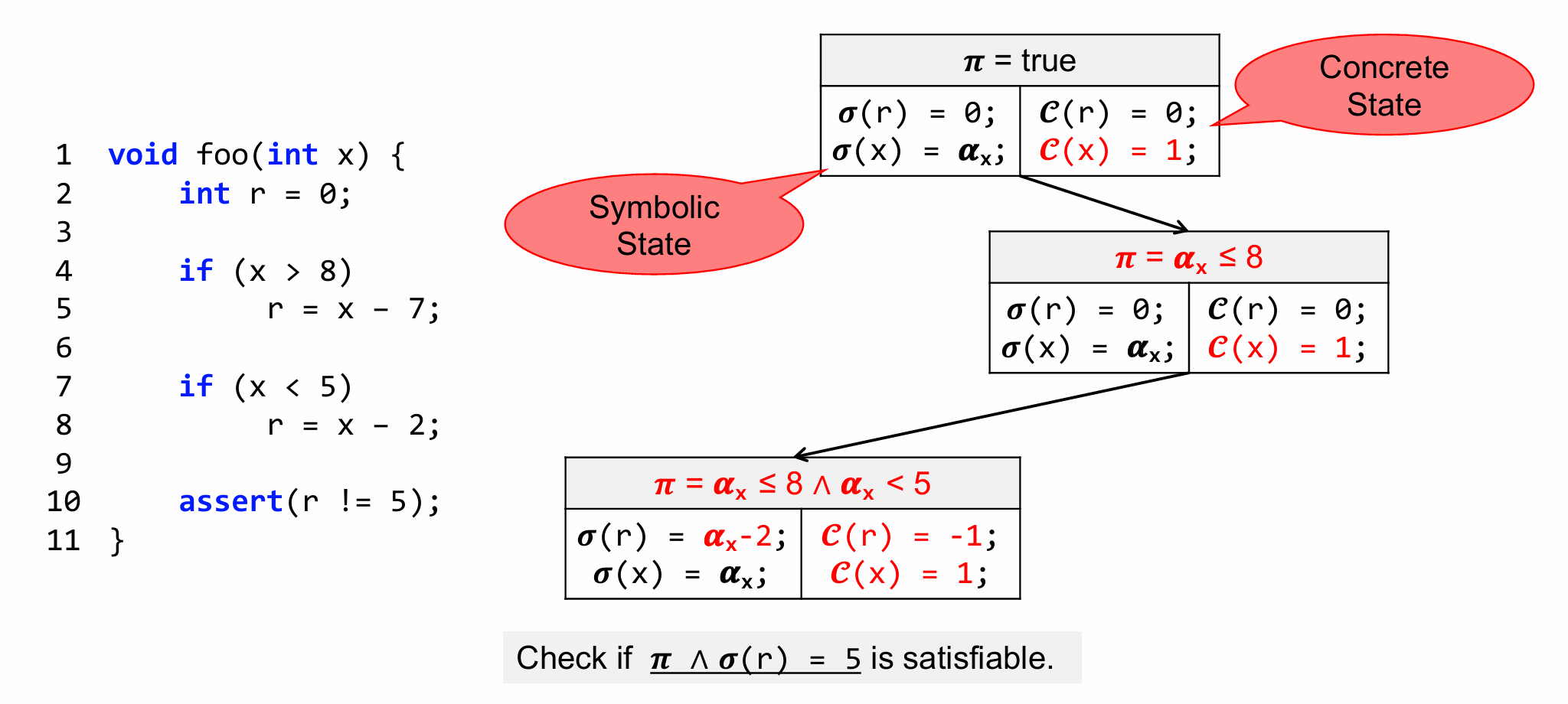
⭐Symbolic Execution

• Path Sensitivity：分析时区分不同执行路径（如条件分支、循环），为每条路径生成独立的状态

• Flow Sensitivity：分析时考虑语句的执行顺序，但忽略不同路径（如条件分支）的差异

• Context Sensitivity：

Symbolic execution is a classic path-sensitive analysis that enumerates and analyzes each path of a program

​ image-20250618171806254

image-20250618192217711

check的时候，为什么最后assert里的式子要取反呢？

当程序执行到 assert(condition) 时，如果 condition 为 false，程序会立即抛出 AssertionError 异常并终止。
这代表程序逻辑与预期严重不符

我们不希望任何输入触发断言失败（即异常），于是符号执行会在程序运行前 静态分析所有路径，并回答关键问题：

是否存在某种输入，使得程序执行到 assert 时，条件为假？

当前路径约束(π) ∧ ¬(cond)，即路径约束 + 断言失败的条件

  • 可满足 → 漏洞！ 存在输入会触发异常。
  • 不可满足 → 安全！ 此路径下断言永真。

问题：Path explosion

​ img

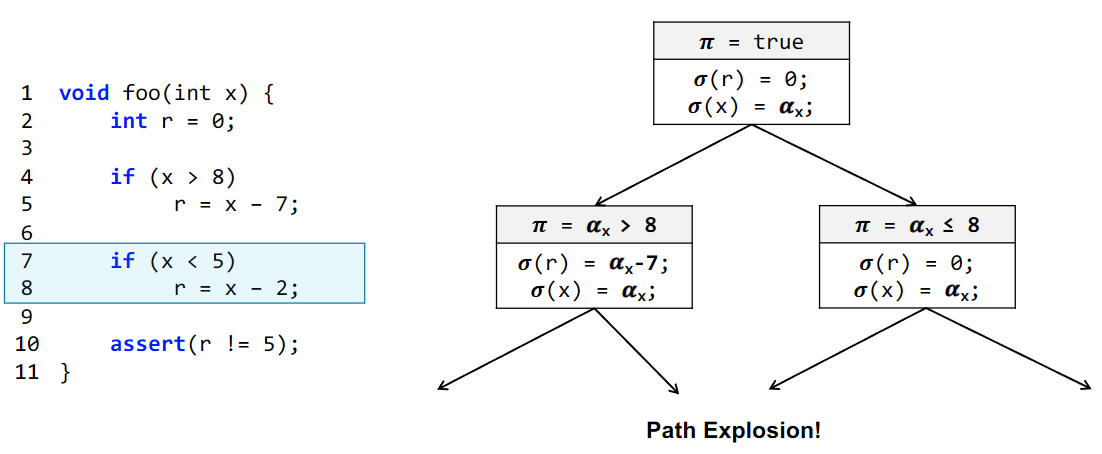
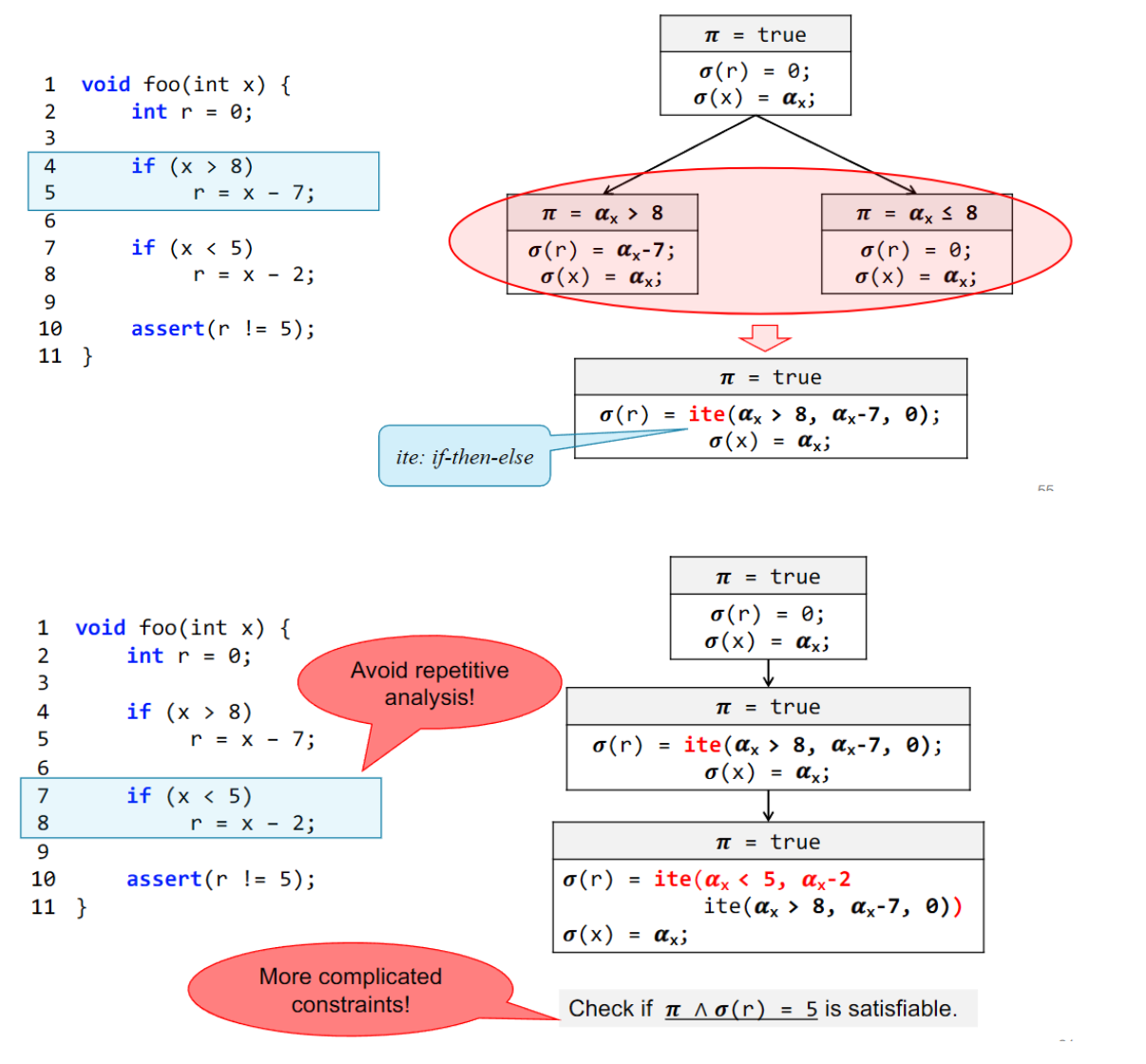
解决方法：合并

​ image-20250618192328034

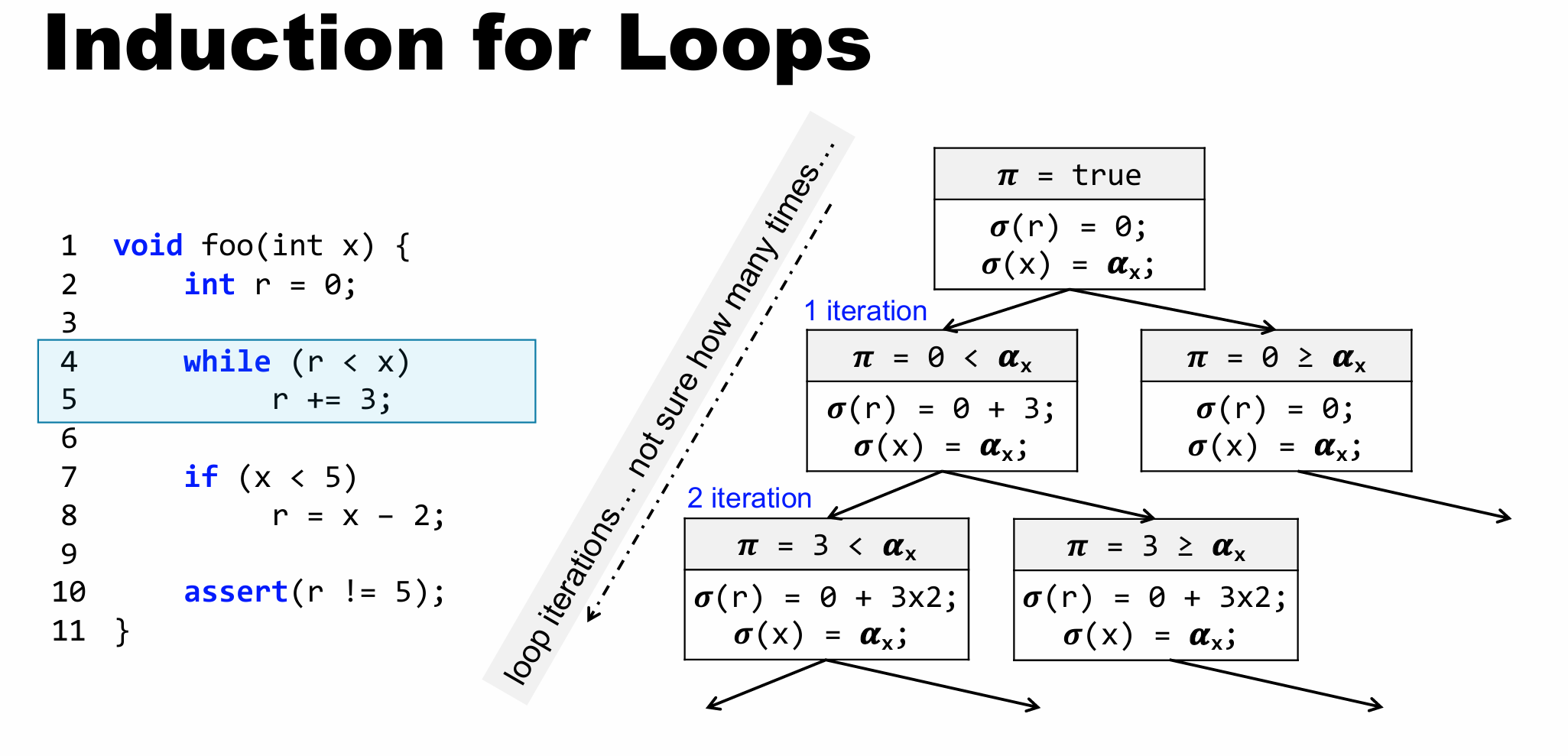
新问题：无限循环

​ image-20250618200130023

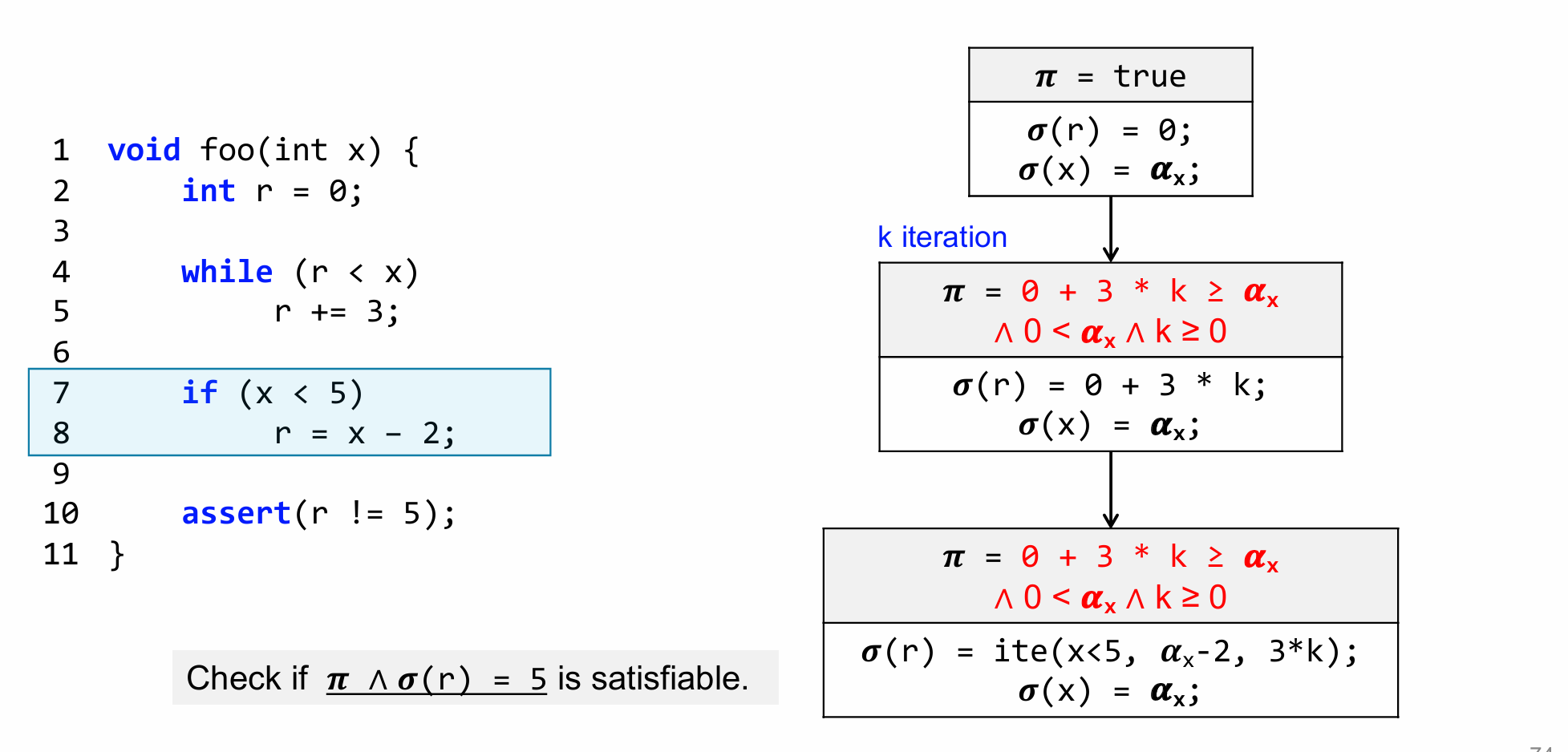
解决方法：

​ image-20250618200233577

Concolic Execution：Concrete + Symbolic Execution运行时进行符号执行

​ image-20250618200400378

Propositional Logic (PL)

​ image-20250618201623523

NNF (Negation Normal Form) - 否定范式

定义：

  • 公式中只允许在原子命题（变量或常量）前出现否定符 ¬。

  • 不允许：¬ 作用于复合表达式（如 ¬(p ∧ q)），也不允许蕴含 ⇒ 和等价 ⟺。

DNF (Disjunctive Normal Form) - 析取范式

CNF (Conjunctive Normal Form) - 合取范式

Tseitin Transformation

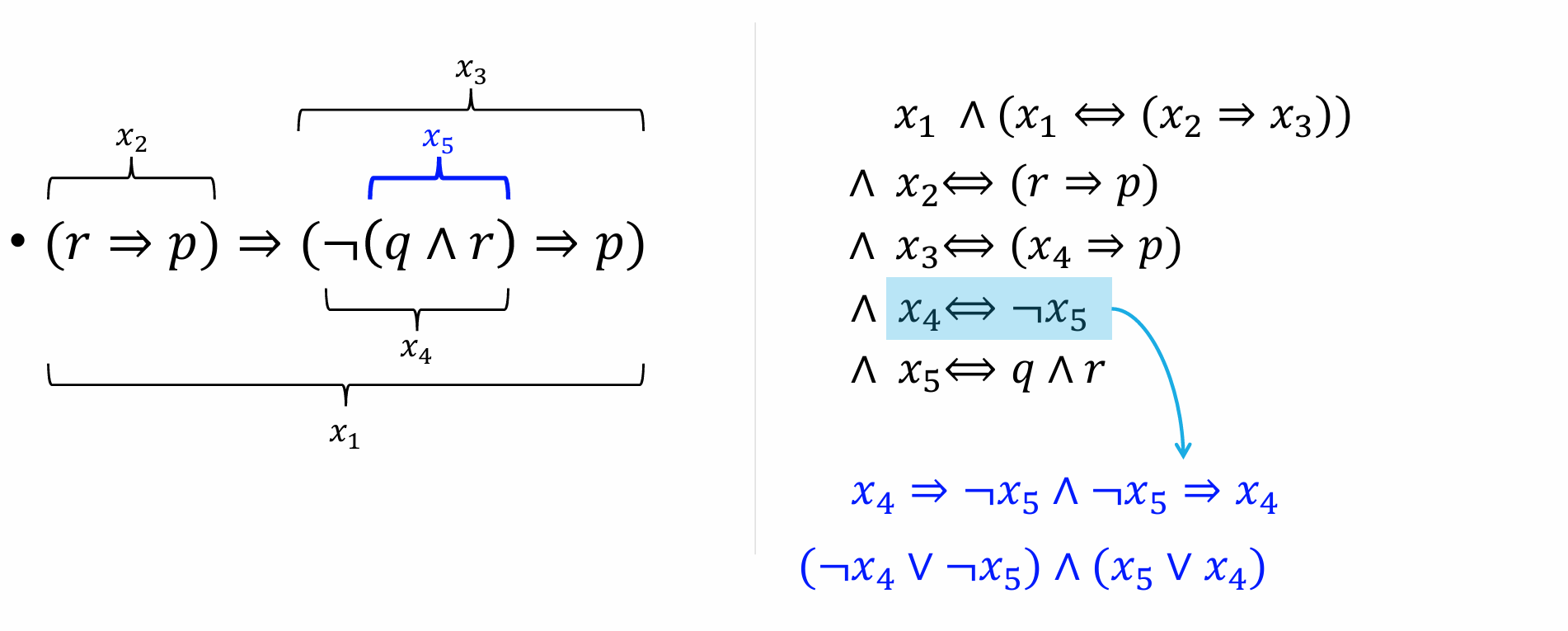
​ image-20250618203820316

SAT

SAT 问题 是指判断一个**命题逻辑公式（PL 公式）**是否存在一组真值赋值（即给所有变量分配 ⊤ 或 ⊥），使得公式计算结果为 ⊤（真）。

DPLL

​ image-20250618204930711

步骤分解

  1. 初始状态：公式：(p ∨ ¬q) ∧ (¬p ∨ r) ∧ (¬r ∨ s)赋值：σ = {}
  2. 决策：选择变量 p（假设按顺序选）
    • 分支 1：尝试p=⊤
      • 单元传播：
        • 子句 (p ∨ ¬q) → ⊤ ∨ ¬q = ⊤ → 删除
        • 子句 (¬p ∨ r) → ⊥ ∨ r = r → 简化为 (r)
        • 强制 r=⊤
      • 子句 (¬r ∨ s) → ¬⊤ ∨ s = s → 强制 s=⊤
      • 公式为空 → SAT！解：p=⊤, r=⊤, s=⊤（q 任意）
  3. 若分支 1 失败：回溯尝试 p=⊥
    • 子句 (p ∨ ¬q) → ⊥ ∨ ¬q = ¬q → 强制 q=⊥
    • 子句 (¬p ∨ r) → ⊤ ∨ r = ⊤ → 删除
    • 子句 (¬r ∨ s) 未简化 → 需继续选择变量（实际已得解，无需此分支）

image-20250618204857185

⭐Pointer Analysis

Andersen & Steensgaard Algorithm

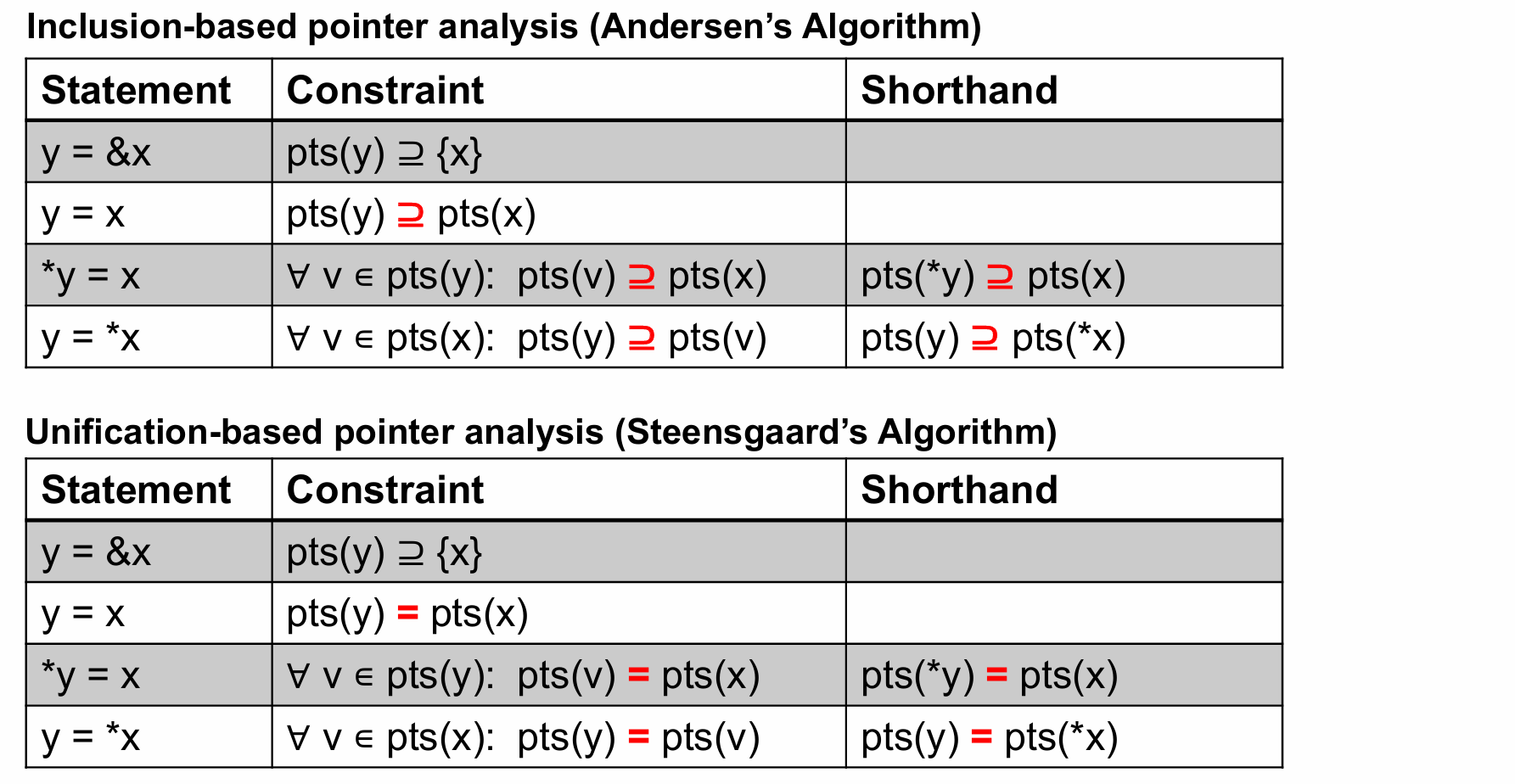
image-20250618210212058

计算**过近似（May）**的指针指向集合（pts(x) = 变量 x 可能指向的对象集合）。

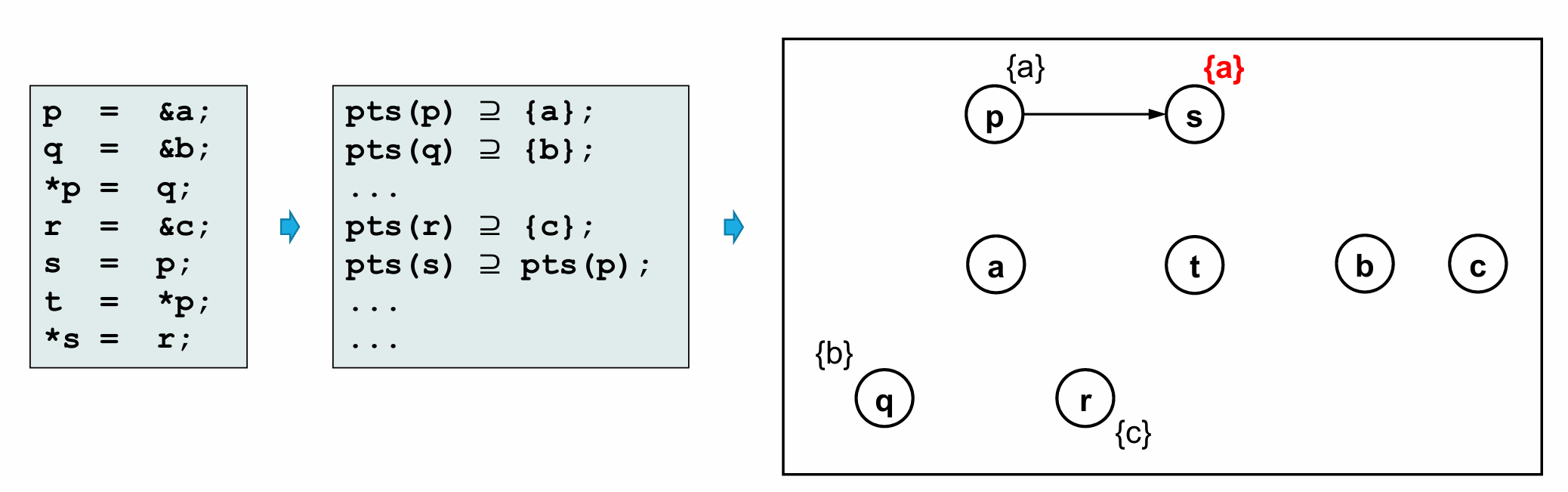
image-20250618211442917

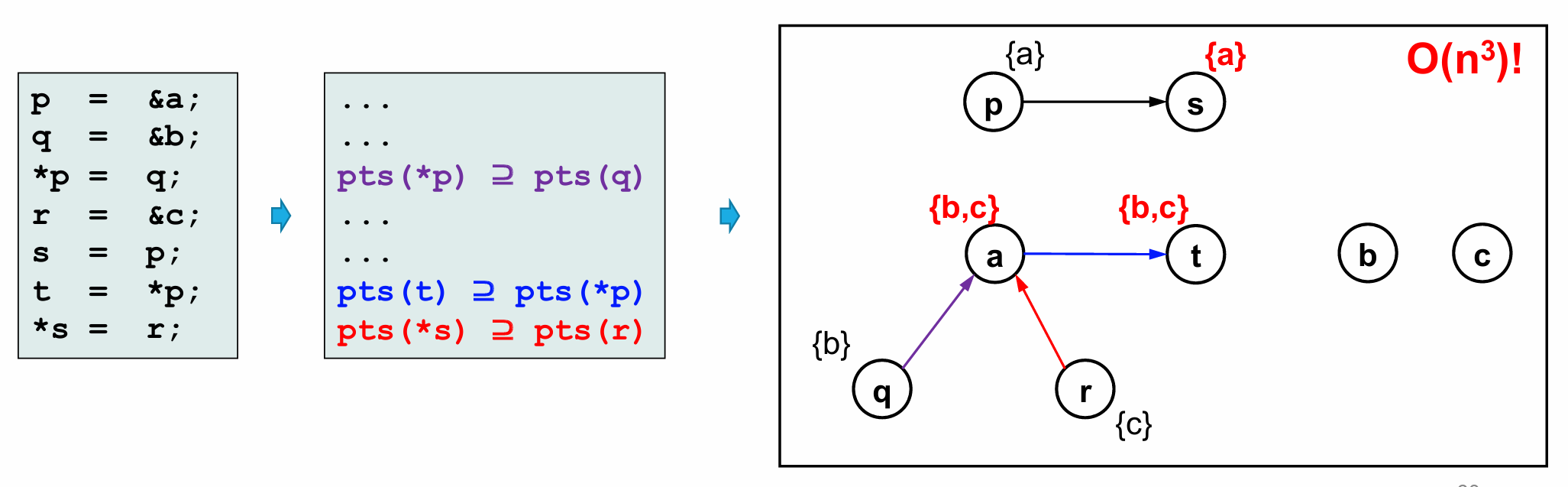
image-20250618212018297

Datalog-Based Analysis

def(B, N, x) 表示"在块 B 的第 N 行定义了变量 x"。

succ(B, N, C)表示C是B的后继且B有N条statement

rd(B, N, C, M, X)C中第M行定义的x在B中第N行使用

几个推导式：

• rd(B, N, B, N, X) :- def(B, N, X)

• rd(B, N, C, M, X) :- rd(B, N-1, C, M, X), def(B, N, Y), X≠Y

• rd(B, 0, C, M, X) :- rd(D, N, C, M, X), succ(D, N, B)

​ image-20250618213057739

image-20250618213121974

The Compilers’ Back End

Instruction Selection

三类指令

​ image-20250618213244542

Addressing Modes

LD R1, a(R2)
LD R1, 100(R2)
LD R1, *R2
LD R1, *100(R2)
LD R1, #100
• LD R, addr
• ST addr, R

image-20250618213503162

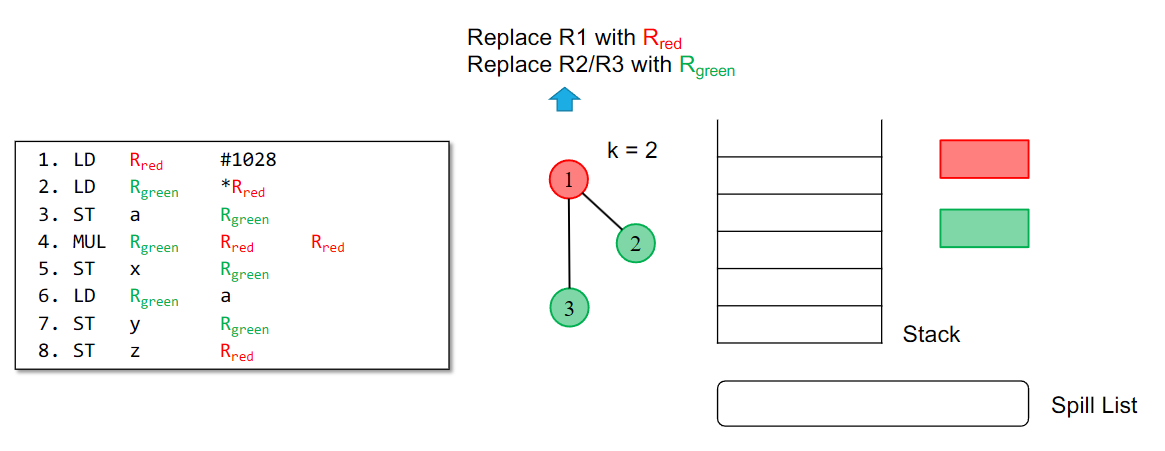
⭐Register Allocation

Local

​ image-20250618213540636

MAXLIVE=4，只需要4个寄存器合理分配就能执行完整个任务（前提是物理寄存器有4个）

​ image-20250618213701769

如果物理寄存器少于4个，比如说3个

​ img

尽量挑选距离下一次使用比较久的spill

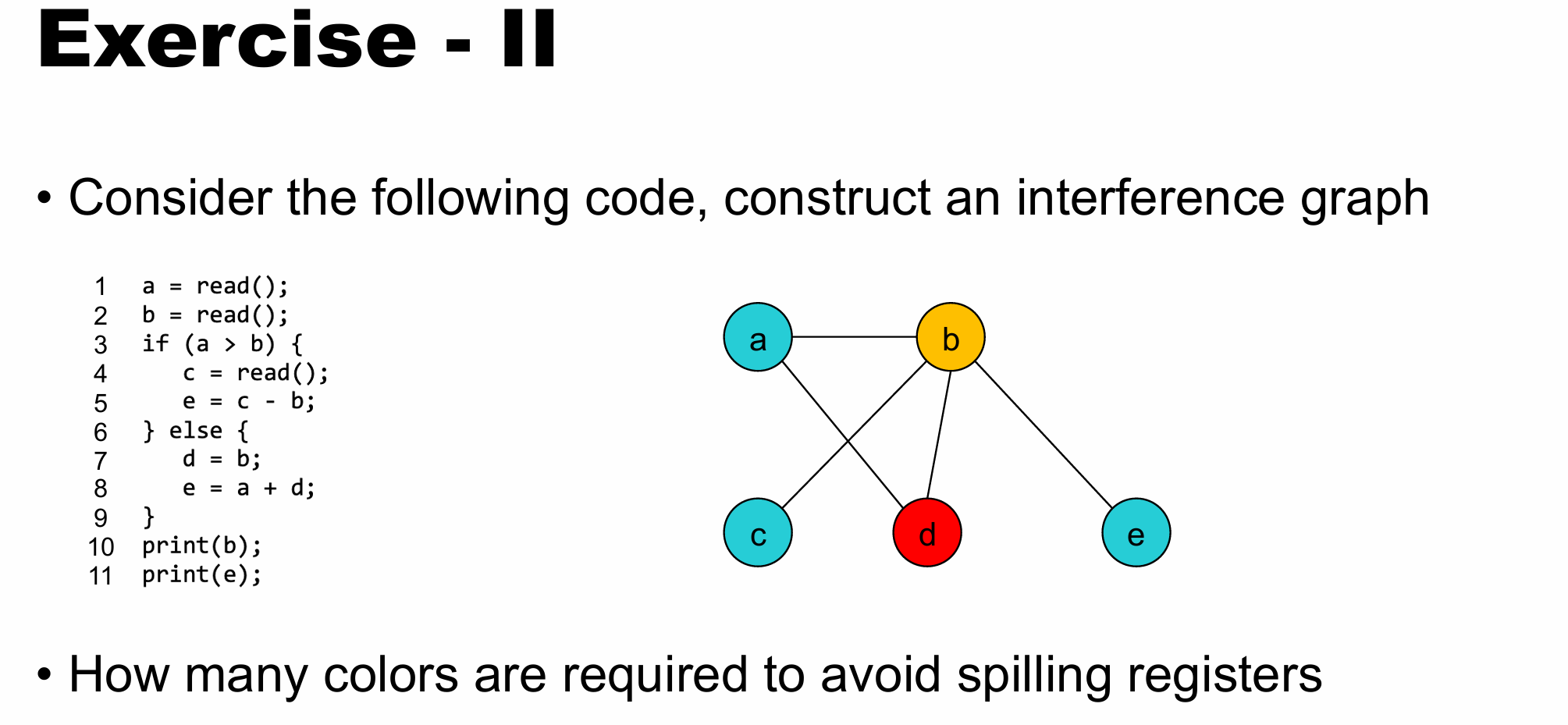
Global

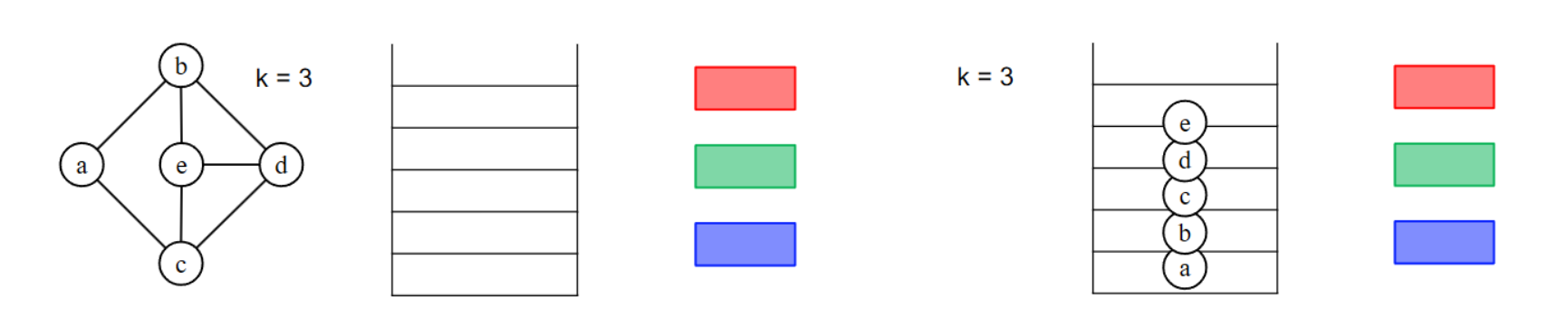
画conflict graph

• Vertex: virtual registers;

• Edges: virtual registers that have overlapping live range

Chaitin’s Algorithm

删除这些顶点并将它们推送到堆栈中，直到图形变为空（稍后为它们着色）

  1. 遍历冲突图，找到所有度数 <k 的节点。
  2. 移除这些节点（因其必然可着色），并压入栈。
  3. 重复直到图中仅剩度数 ≥k 的节点或图为空。

image-20250618214555560

若有度数 ≥k 的节点

  1. 将溢出候选节点加入溢出列表（Spill List）
  2. 重复上步骤
img

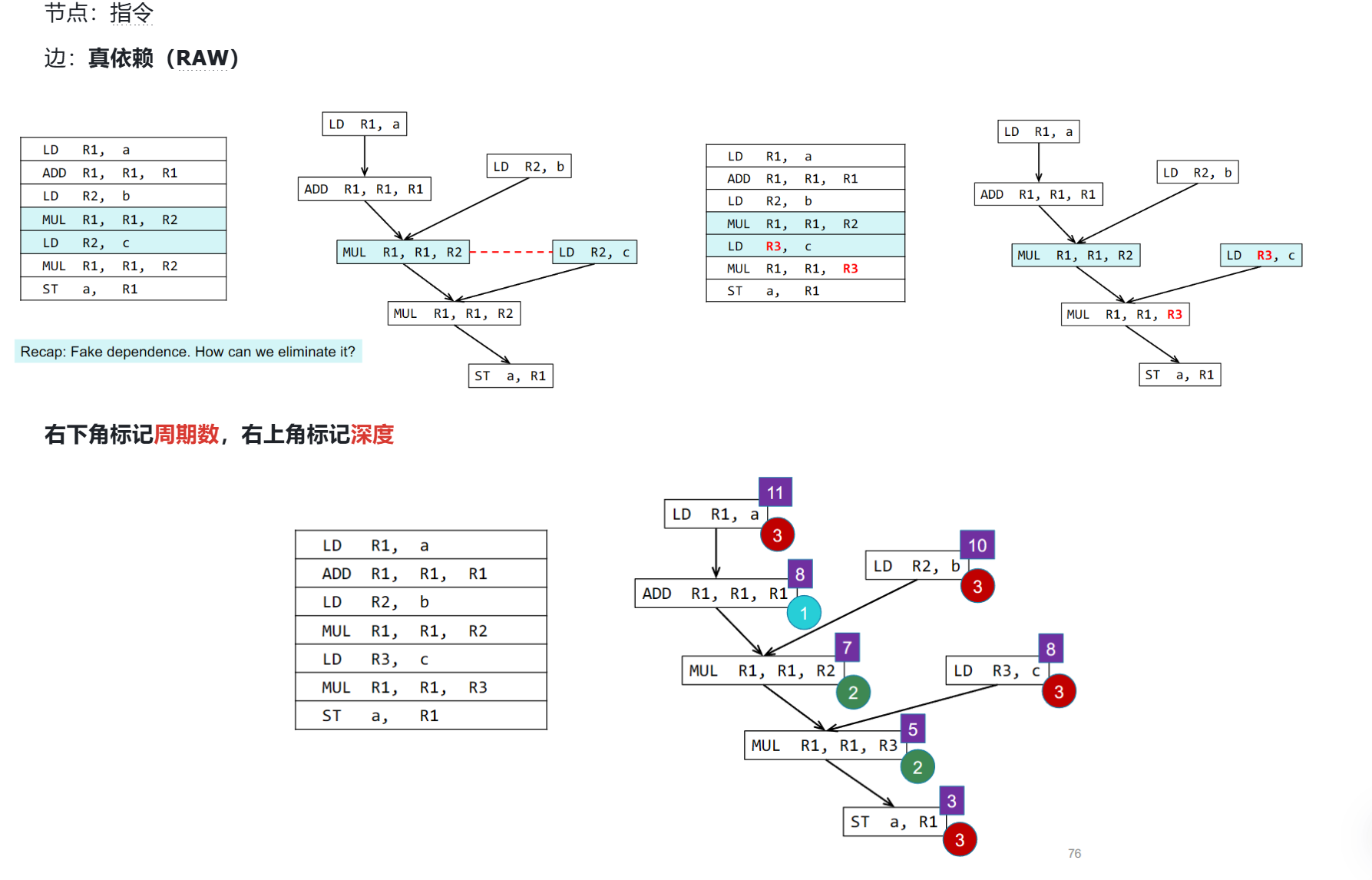
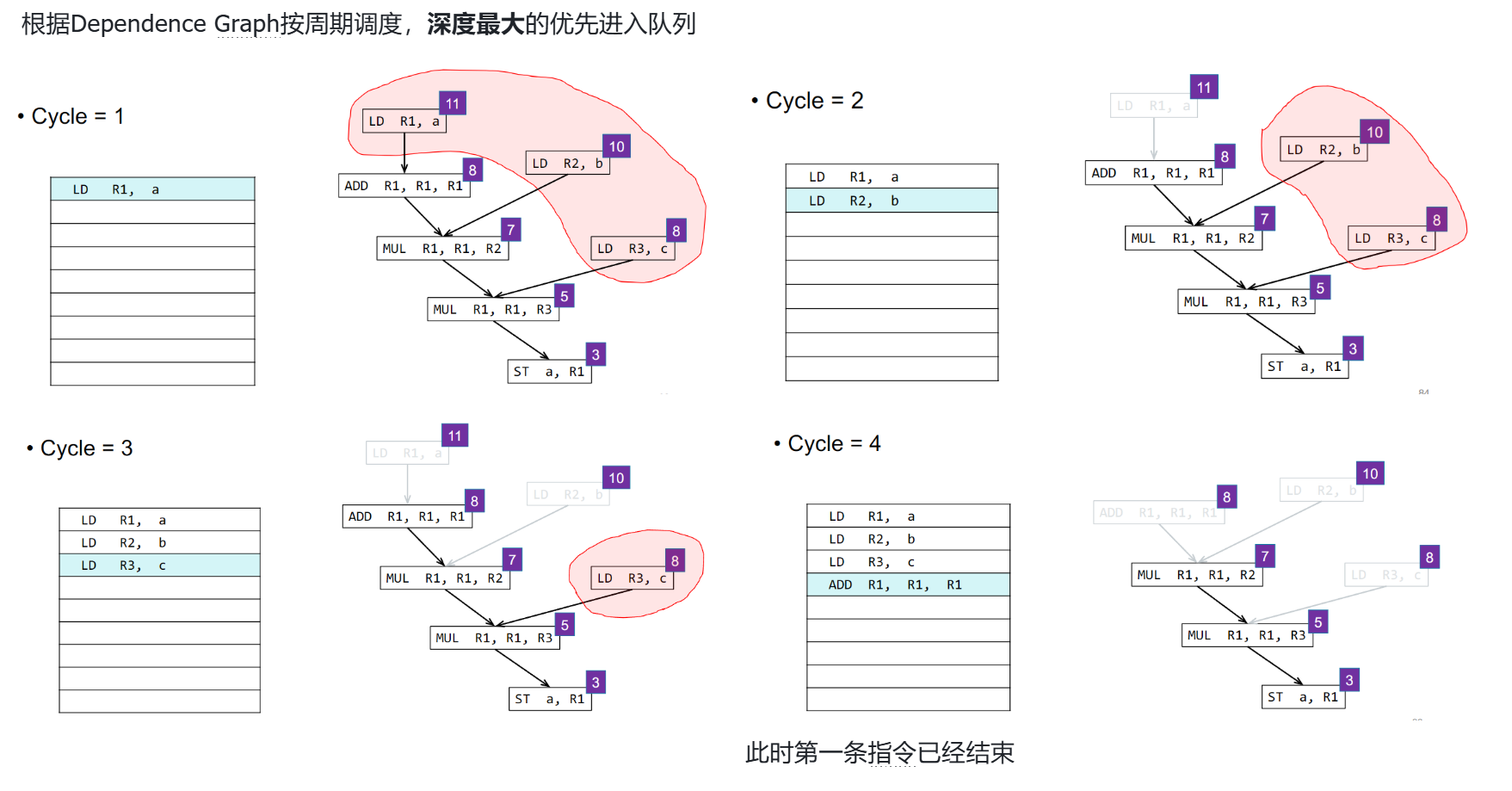
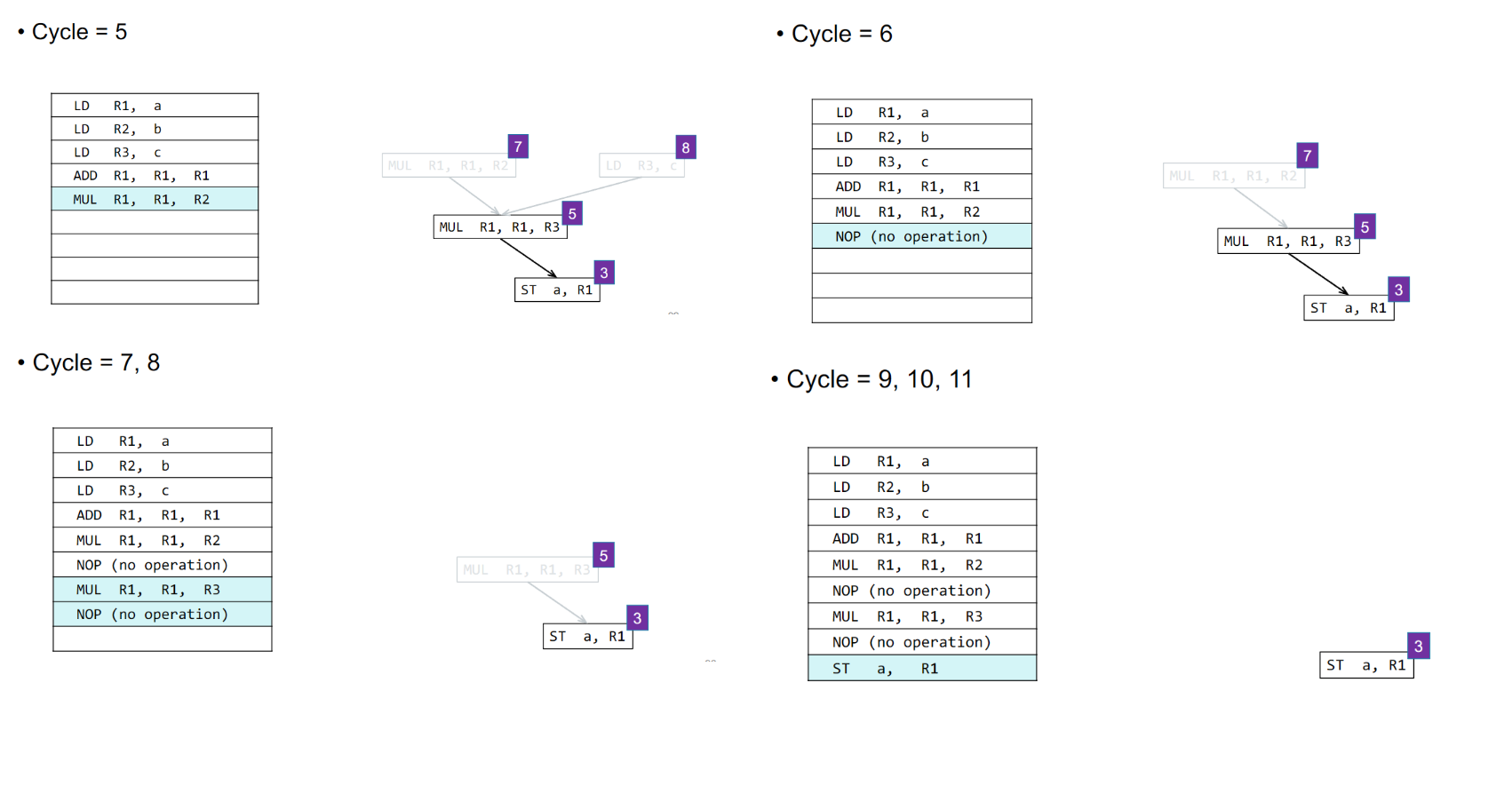
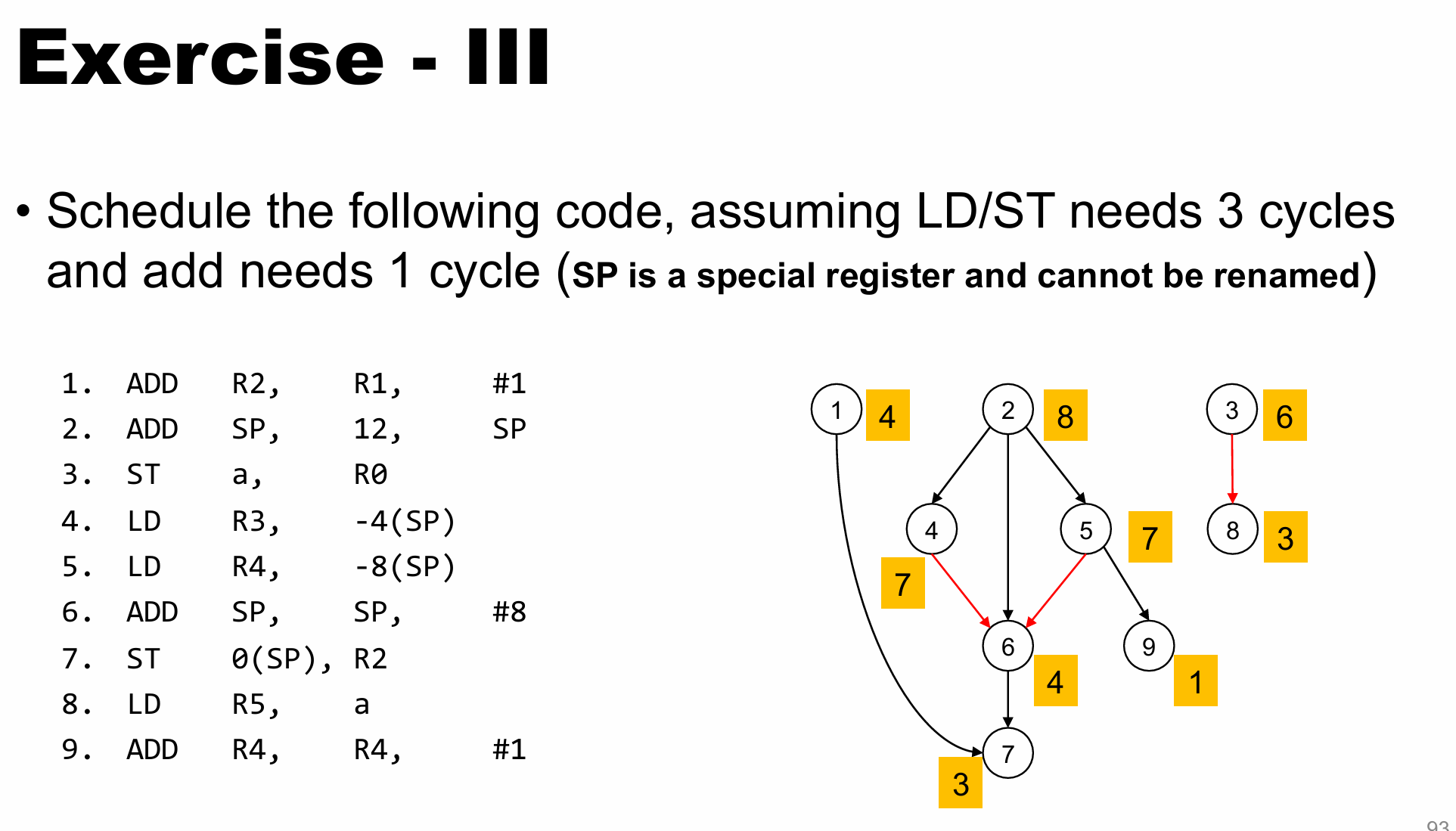
⭐Instruction Scheduling

True/Fake Dependence

具体类型：

  • RAW（Read After Write）：指令A写入的数据被指令B读取，B必须在A完成后执行。
  • WAR（Write After Read）：指令A读取的数据被指令B写入，A必须在B修改数据前完成读取。
  • WAW（Write After Write）：指令A和指令B写入同一目标（寄存器或内存），必须按程序顺序提交结果。

目标：通过重命名来删除（假）依赖（WAR，WAW），保留真依赖（RAW）

Dependence Graph

image-20250618215018308

image-20250618215111436

image-20250618215119873

image-20250618215612290

image-20250618215622674

image-20250618215638424