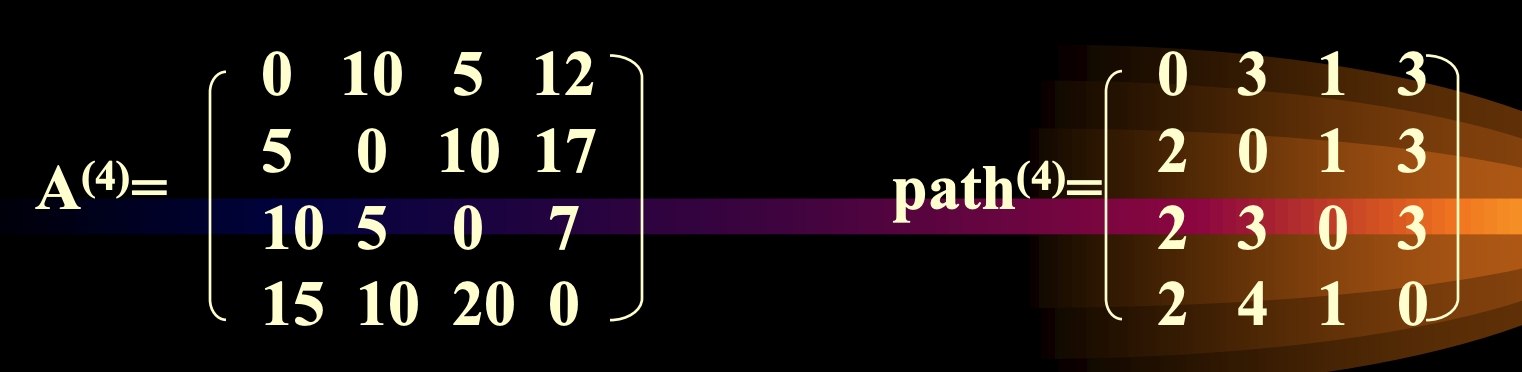数据结构与算法2024重点
编程题2大题 Java或者c++
最短路径算法
第一章
概念不考文字默写
算法概念不考?
递归
汉诺塔?可能有选择
public static void hanoi(int num, char a, char b, char c) { if (num == 1) { System.out.println("第" + num + "个圆盘从" + a + " -> " + c); } else { hanoi(num - 1, a, c, b); System.out.println("第" + num + "个圆盘从" + a + " -> " + c); hanoi(num - 1, b, a, c); } }
范型不考
第二章
大O表示法和量级,会看复杂度
$\Omega$表示法看一下
$T(N) = O(f(N)),表示T(N)的增长率$小于等于$f(N)$
$T(N) = \Omega(f(N)),表示T(N)的增长率$大于等于$f(N)$
$T(N) = \Theta(f(N)),表示T(N)的增长率$等于$f(N)$
分治
先分后治:划分成子问题(一般两个)在将两个解决的子问题合并到一起
典型:折半查找、归并排序
第三章
ADT概念不考,理解
链表,栈,队列,数组等
单链表、栈、队列:高概率
双向链表好像不考
循环链表? 约瑟夫问题好像不考
所有排序都要看
栈的数组实现不考
第四章
概念不考
满、完全二叉树了解
*广义表不考
==遍历(递归和非递归算法)==非递归好像不考?
树:
深度优先遍历
先序次序遍历(先序) 访问树的根 按先序遍历根的第一棵子树,第二棵子树, ……等。
中序
后序次序遍历(后序) 按后序遍历根的第一棵子树,第二棵子树,……等 访问树的根。
广度优先遍历
分层访问
二叉树:
先序:
StringBuilder sb = new StringBuilder(); if (root != null) { sb.append(root.element); sb.append(PreOrderTraversal(root.left)); sb.append(PreOrderTraversal(root.right)); }中序:
StringBuilder sb = new StringBuilder(); if (root != null) { sb.append(InOrderTraversal(root.left)); sb.append(root.element); sb.append(InOrderTraversal(root.right)); }后序:
StringBuilder sb = new StringBuilder(); if (root != null) { sb.append(PostOrderTraversal(root.left)); sb.append(PostOrderTraversal(root.right)); sb.append(root.element); }实际上就是改变访问节点的顺序
非递归算法:
中序: 无限循环,每次把当前节点的左子树压入栈,然后如果栈不为空,就弹出一个表示当前访问的节点,然后p = p->right;这样下一次循环的时候就又会把右子树的左子树都压入栈
后序: 无限循环,给根节点添上tag位(用来记录是否是从该节点的右子树回到该节点的),压左子树时tag=0,如果tag=1输出并弹栈,如果tag!=0, p = p -> right
建立树MakeTree不考,由序列构造二叉树看一看,后缀表示好像不考
序列构造二叉树(先序和中序):
public static BinTree CreateBT(char[] pres, char[] ins){ // please enter your code here... if (pres.length == 0) return null; char rootValue = pres[0]; BinTree root = new BinTree(rootValue, null, null); int rootIndex = 0; for (int i = 0; i < ins.length; i++) { if (ins[i] == rootValue) { rootIndex = i; break; } } root.left = CreateBT(Arrays.copyOfRange(pres, 1, 1 + rootIndex), Arrays.copyOfRange(ins, 0, rootIndex));//pres中根节点后的前rootindex个元素 , ins中的rootindex前的元素 root.right = CreateBT(Arrays.copyOfRange(pres, 1 + rootIndex, pres.length), Arrays.copyOfRange(ins, rootIndex + 1, ins.length)); return root;// 剩余元素 }
字符串翻一翻
串:是n(n>=0)个字符的一个有限序列,开头结尾用双引号“ ”括起来
*串的长度:串中所包含的字符个数n(不包括分界符‘ “ ’,也不包括串的结束符‘\0’)
*空串:长度为0的串。或者说只包含串结束符‘\0’的串 注意:“\0 ”不等于“ \0 ”, 空串不等于空白串
*子串:串中任一连续子序列
例子:B= “peking ”,,则空串“ ”、“ki ”、“peking ”都是B 的子串,但“pk ”不是B的子串
双亲、左子女右兄弟表示法并查集
左子女右兄弟表示(InsertChildren):
这里current表示父节点
TreeNode<T>*newnode = new TreeNode<T>(value); if(current->firstchild = = NULL) current->firstchild = newnode; else { TreeNode<T>*p = current->firstchild; while ( p->nextsibling!=NULL) p = p->nextsibling; p->nextsibling = newnode; }
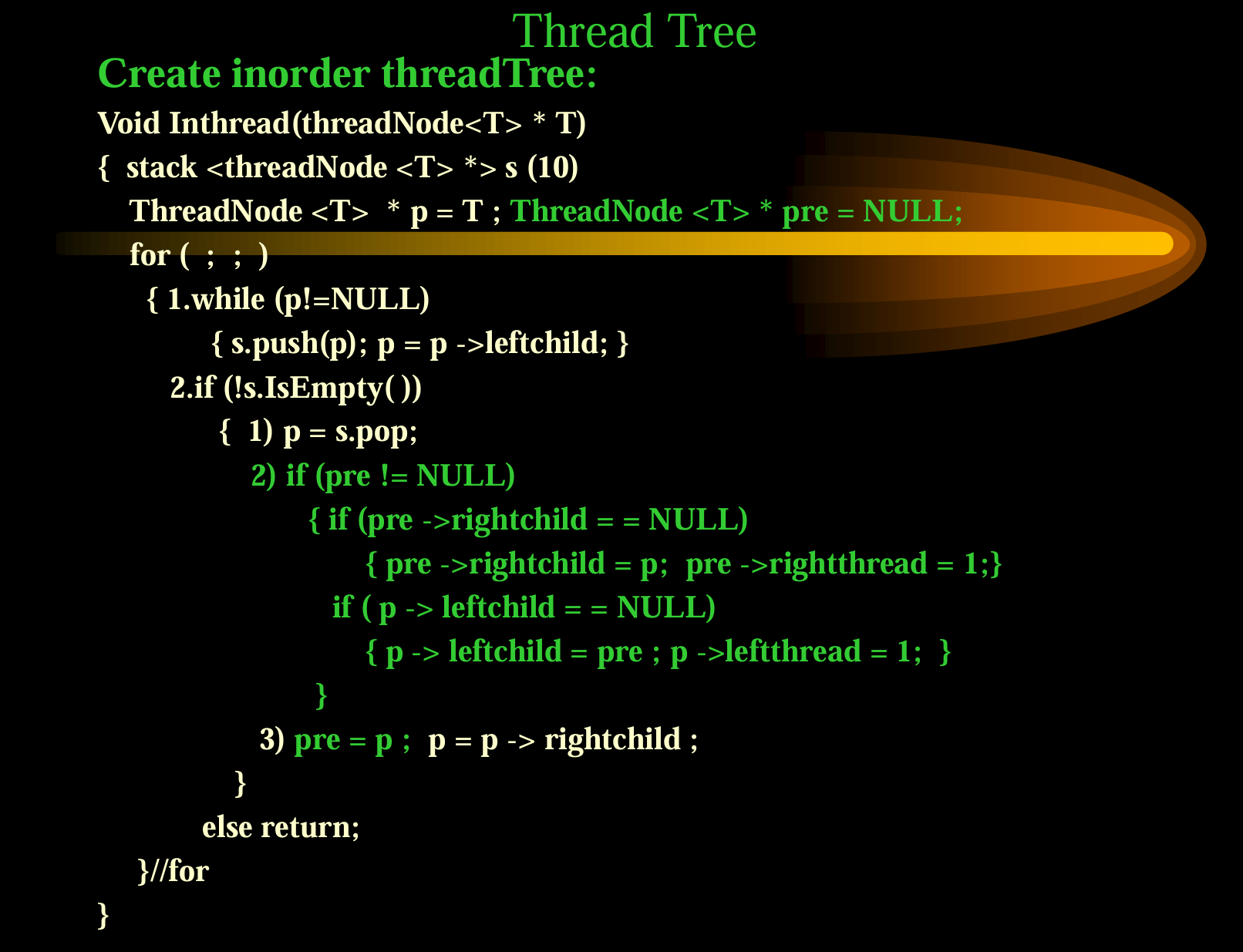
线索树(例题参考课后考研题)

First( ) { while (current->leftThread= =0) current=current->leftchild; return current; } Next( ) { ThreadNode<Type>* p=current->rightchild;//此时不确定rightchild是右子树的根节点还是后继 if(current->rightThread= =0)//是右子树的根节点 while(p->leftThread= =0) p=p->leftchilld;//找后继 current=p;//设为后继 }创建中序线索树:
霍夫曼树、霍夫曼编码
构建霍夫曼树,权值大的靠近根节点
可以将权值最小的W1、W2合并成W=W1+W2作为新的节点看待
搜索树
AVL平衡树、B树
AVL插入:
比当前节点大往左插,小往右插,平衡
平衡:相对大小顺序不变,依然保持二叉树的结构
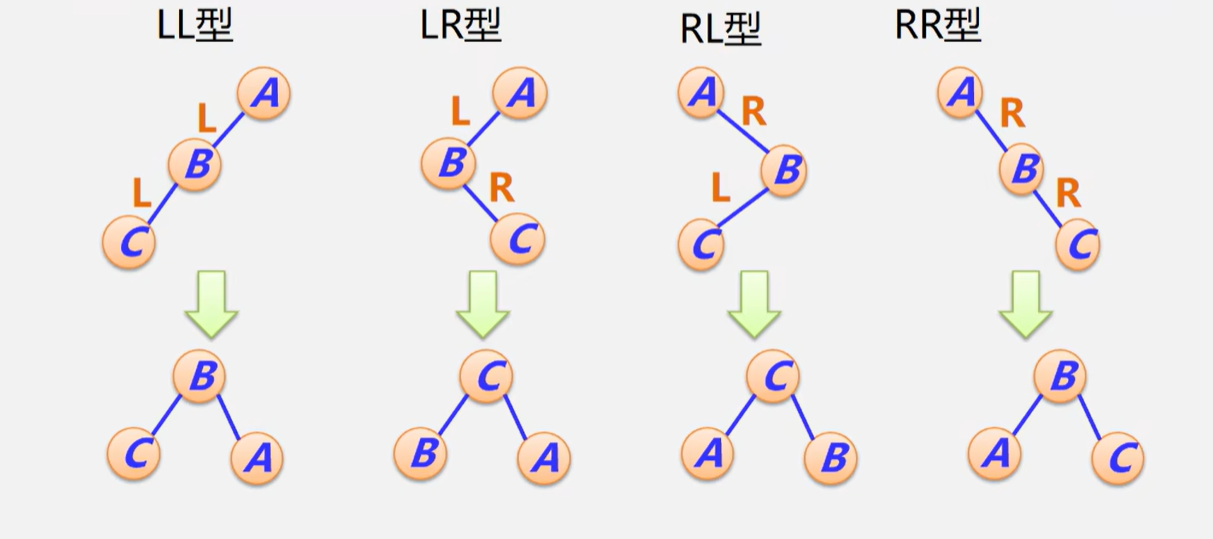
LL:B的右节点(如果有的话,大小一定介于B和A之间),为保持性质,要接到A的左子树
LR: 同理,C的左右节点分别接到B的右和A的左
RL:C的左右节点分别接到A的右和B的左
RR:B的左节点接到A的右
private AVLNode insert( Comparable x, AVLNode t ) { if ( t = = null ) t = new AVLNode( x, null, null );//递归结束点,插入新节点 else if ( x.compareTo( t.element ) < 0 ) { t.left = insert( x, t.left ); //递归 if( height( t.left ) – height( t.right ) = = 2 )//找最小不平衡点 if( x.compareTo( t.left.element ) < 0 ) t = rotateWithLeftChild ( t );//LL else t = doubleWithLeftChild( t );//LR }else if( x.compareTo( t.element ) > 0 ) { t.right = insert( x, t.right ) ; if( height( t.right ) – height( t.left ) = = 2 ) if( x.compareTo( t.right.element ) > 0 ) t = rotateWithRightChild( t );//RR else t = doubleWithRightChild( t );//RL } else ; t.height = max( height( t.left ), height( t.right ) ) + 1; return t; }删除节点:
若为叶子,直接删
若只有一个子树,子树代替位置
若左右子树都有,用前驱或者后继节点顶替
B树:好像的好像不考???
第五、六章
散列表、优先队列、并查集、堆 不一定会考,可能挑一部分考,随机
散列表:平方取中好像没出
杂没考
开放地址线性探测

二次探测好像没出
再散列 看看
分离链接 看看
堆: 堆排序O(n log n)
上滤下滤
建堆算法O(n)
调整时间O(log n)
堆 : 看作一棵顺序存储的完全二叉树
堆排序:
public static void heapsort( Comparable [ ] a ) { // 1. 从最后一个 "非叶子节点" 开始,依次向上调整每个子堆 for( int i = a.length / 2; i >= 1; i-- ) percDown( a, i, a.length ); // 2. 逐步将最大值(堆顶)移到数组末尾,并重新调整堆 for( int i = a.length; i > 1; i-- ) { // 将当前堆的堆顶元素(最大值)与当前堆的最后一个元素交换 swapReferences( a, 1, i ); // 重新调整剩余的堆,使其仍然是最大堆 percDown( a, 1, i-1); } } private static void percDown( Comparable [ ] a, int i, int n ) { int child; Comparable tmp; // 用 `tmp` 保存当前节点的值 for( tmp = a[ i ]; leftChild( i ) < n; i = child ) { child = leftChild( i ); // 找到当前节点的左子节点 // 如果右子节点存在并且比左子节点大,选择右子节点 if( child != n – 1 && a[child ].compareTo( a[ child + 1 ]) < 0 ) child++; // 如果子节点比当前节点大,则将子节点上移 if( tmp.compareTo( a[ child ] ) < 0 ) a[ i ] = a[ child ]; else break; // 已经满足堆性质,退出循环 } // 将原来的值 `tmp` 放到最终位置 a[ i ] = tmp; } private static int leftChild( int i ) { return 2 * i + 1; }O(nlogn)
第七章
好像没考
第八章
最短路径
Dijkstra 算法(非負權值單源最短路徑)
圖中所有邊的權值非負(>=0)
計算圖中某點 v0 到其他各點 vi 的最短路徑
步驟
- 選擇起始點 v0,使 S = {v0},E = {},E’ 為 p:s, vi(s 為 S 中的點),即 S 中元素到非 S 中元素的最短邊的集合
- 選擇權值(代價)最小的邊 ei 加入 E,即 E = union(E, {ei}),S = union(S, {vi})
- E 中的元素必表示 v0 到 s 的最短距離(s 為 S 中元素)
- 更新 E’ 集合,重複2,3步驟直到所有點的最短距離都找到
void Graph::shortestpath(int n,int v){ for( int i=0; i<n; i++){ //初始将除v外所有点设为为加入 dist[i]=Edge[v][i]; s[i]=0; //s[i]==1表示点i已加入 if( i!=v && dist[i]< MAXNUM ) path[i]=v; else path[i]=-1; } s[v]=1; dist[v]=0; // s | 1 | 0 | 0 | // dist | 0 | . | . | // path | -1 | . | . | for( i=0; i<n-1; i++){ //共遍历n-1次 float min=MAXNUM; int u=v; for( int j=0; j<n; j++)//选择未加入的最近的点加入 if( !s[j] && dist[j]<min ) { u=j; min=dist[j]; } s[u]=1; for ( int w=0; w<n; w++)//计算经过新点到其他点的距离 if( !s[w] && Edge[u][w] < MAXNUM && dist[u]+Edge[u][w] < dist[w]){ //未加入 且 有直连边 且 路径更短 dist[w]=dist[u]+Edge[u][w]; path[w]=u; } }//for }
- 複雜度:O(n^2)
Bellman-Ford 算法(任意權值單源最短路徑)(貝爾曼-福特)
- 構造最短路徑長度數組,dist^i[u]為從源點(起點)經過 i 條邊到達 u 的最短路徑長度
- 帶負權值邊不可構成迴路(v0 [+a]-> v1 [-b] -> v0,相當於不動而長度自減)
void Graph::BellmanFord(int n, int v){ for(int i=0;i<n;i++){ dist[i]=Edge[v][i]; if(i!=v&&dist[i]<MAXNUM) path[i]=v; else path[i]=-1; } for (int k=2;k<n;k++) //dist^k(u) 表示从源点v最多经过不构成带负长度边回路的n-1条边的最短路径长度; for(int u=0;u<n;u++) if(u!=v) for(i=0;i<n;i++)//遍历其他顶点 if (i!=u && Edge[i][u]<MAXNUM && dist[u]>dist[i]+Edge[i][u]{ //原有路径长 <?> v到i的最短路径+i到u的边 dist[u]=dist[i]+Edge[i][u]; path[u]=i;//u的前驱就是i了 } }
- 複雜度:O(n^3)
Floyed 算法 所有頂點的最短路徑(非負權值)
- 計算所有頂點的最短路徑和
- 執行 Dijkstra 算法 n 次
- Floyed 算法
複雜度:都是 O(n^3)
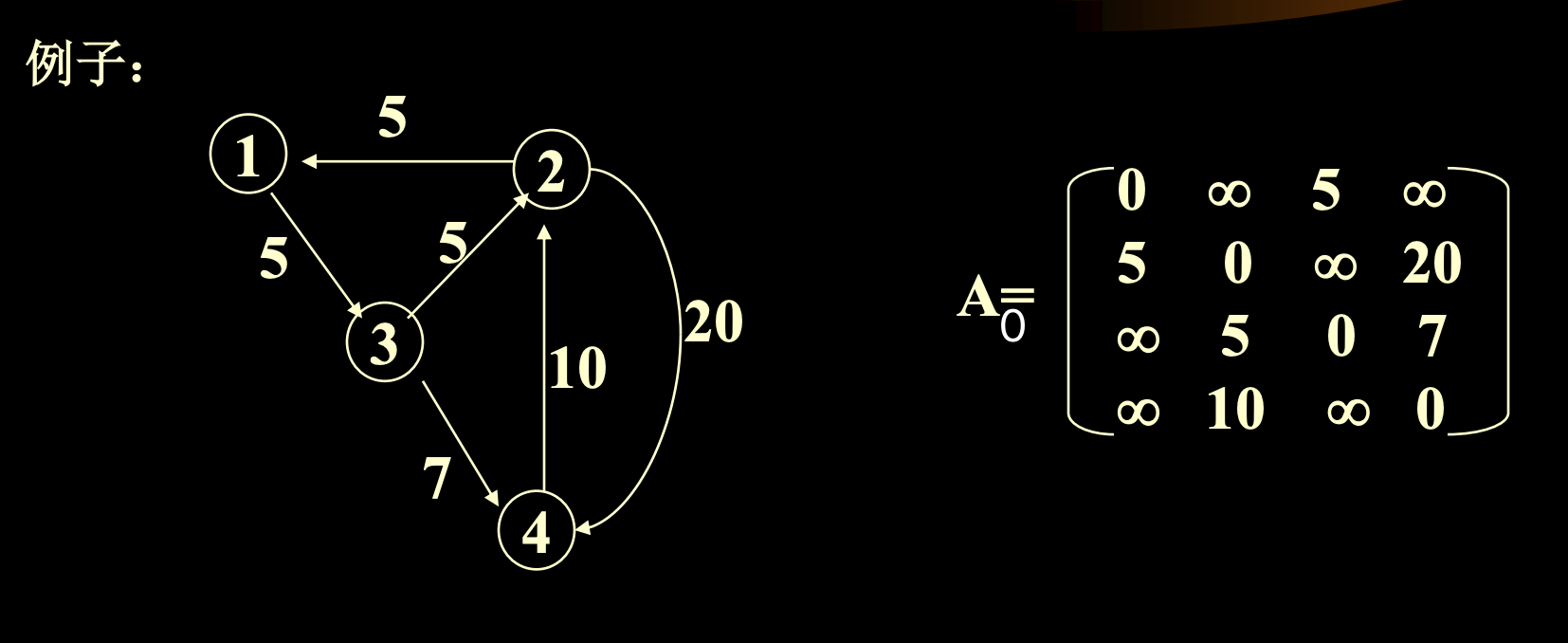
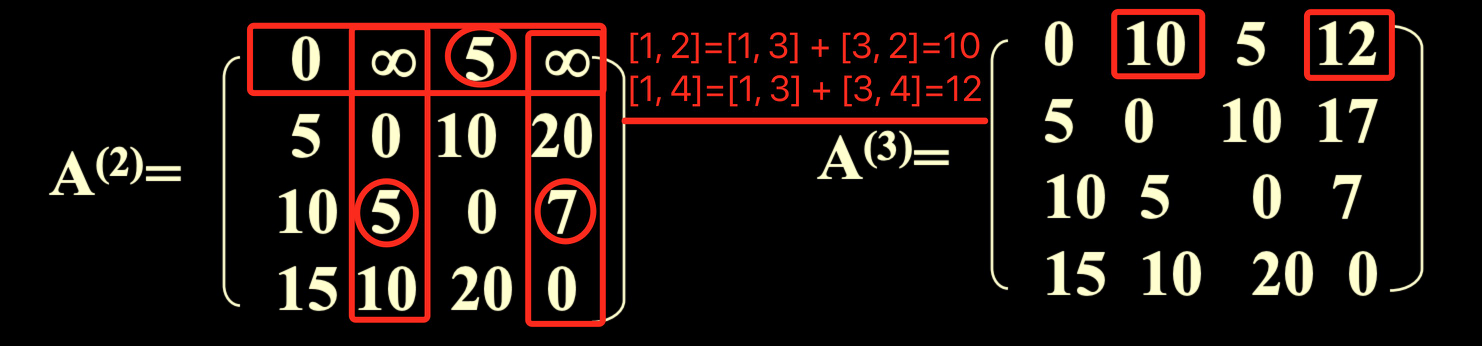
Floyed 算法步驟
- 以鄰接矩陣表示,初始矩陣為 A0,自反邊長度為 0,未連通視為無限
- 作 n-1 次迭代(路径最多长 n-1),每次令 Ai[i, j] = min(Ai-1[i, j], Ai-1[i, 1] + Ai-1[1, j]),即上次迭代最短路徑(<v0, vi-1>)與再經過一條邊(<v0, vk, vi-1>)的路徑取最小值作為新的最短路徑(<v0, vi>)
void Graph::Alllength(int n){ for(int i=0; i<n; i++) for(int j=0; j<n; j++){ a[i][j]=Edge[i][j]; if(i==j) a[i][j]=0; if(i< >j&&a[i][j]<MAXNUM) path=i; //直连 else path[i][j]=0; } for(int k=0; k<n; k++) for(int i=0; i<n; i++) for(int j=0; j<n; j++) if( a[i][k]+a[k][j]<a[i][j] ){ a[i][j]=a[i][k]+a[k][j]; path[i][j]=path[k][j]; // i -> j => i -> k -> j } }
邻接矩阵邻接表
邻接多重表好像没考
遍历算法
DFS Depth First Search 深度优先算法
- 访问顶点 v0,然后访问其中一个未被访问的子顶点,递归访问
- 若不存在未被访问的子顶点,退回到路径上含有未被访问子顶点的顶点,访问未被访问的子顶点,递归实现。
template<NameType,DistType> void Graph<NameType,DistType> :: DFS(int v,visited[]){ cout<<GetValue(v)<<''; visited[v]=1; int w=GetFirstNeighbor(v); while (w!=-1){ if(!visited[w]) DFS(w,visited); w=GetNextNeighbor(v,w); } }
- **算法複雜度:**邻接表 O(n + e),邻接矩阵 O(n^2)
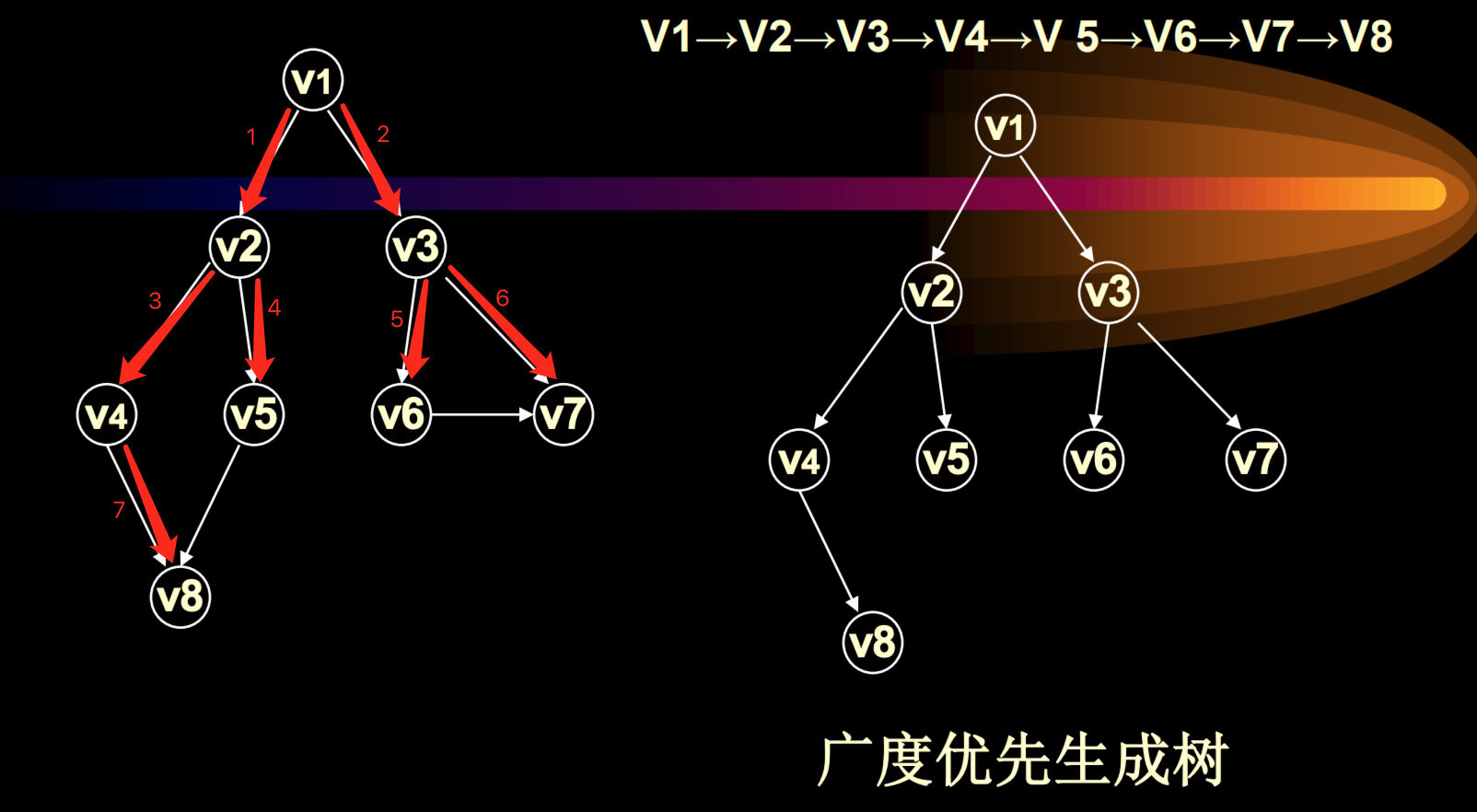
BFS Breadth First Search 广度优先遍历
- 访问顶点 v0,先访问 v0 的所有子顶点 v1, v2, …, vk,然后依序访问 vi(i=1~k)中沒有被访问过的子顶点,非递归实现。
template<NameType,DistType> void Graph<NameType,DistType> :: BFS(int v){ int* visited=new int[NumVertices]; for (int i=0; i<NumVertices; i++) visited[i]=0; cout<<GetValue(v)<<''; visited[v]=1; queue<int> q; q.EnQueue(v); while(!q.IsEmpty()){ v=q.DeQueue(); int w=GetFirstNeighbor(v); while (w!=-1){ if(!visited[w]){ cout<<GetValue(w)<<''; visited[w]=1; q.EnQueue(w); } w=GetNextNeighbor(v,w); } } delete[] visited; }
- **算法複雜度:**邻接表 O(n + e),邻接矩陣 O(n^2)
最小生成树
Prim 算法 :
选点
O(n^2)
Kruskal:
选边
建立e条边的最小堆。
检测邻接矩阵O(n2)
每插入一条边,执行一次 fiterup( ) 算法:log2e
所以,总的建堆时间为O(elog2e)
构造最小生成树时: e次出堆操作,每一次出堆,执行一次filterdown(), 总时间为O(elog2e)
2e次find操作:O(elog2n)
n-1次union操作:O(n)
所以,总的计算时间为O(elog2e+elog2n+n2+n)
AOV、AOE 拓扑排序 时间
拓扑排序:
- 寻找图中入度为 0 的节点 ei(存在多个则次序任意)
- 刪除 ei 与所有 ei 的出边
- 递归直到所有节点都被消去,删除顺序即为拓扑排序
最早时间:V0 -> Vi的最长路径
最晚时间: Vn-1 -> Vi的最长路径
证明不考
第九章
所有排序都要看
插入
public static void insertionSort( Comparable [ ] a ){ int j; for ( int p = 1; p < a.length; p++ ){ Comparable tmp = a[ p ]; for ( j = p; j > 0 && tmp.compareTo( a[ j – 1 ] ) < 0; j-- ) a[ j ] = a[ j – 1 ]; //temp前比temp大的数挨个往后挪 a[ j ] = tmp; } }O(n^2)
折半插入排序好像没出
template <class Type> void BinaryInsertSort( datalist<Type> &list){ for (int i=1; i<list.currentSize; i++) BinaryInsert(list, i); } template <class Type> void BinaryInsert( datalist<Type> &list, int i){ int left=0, Right=i-1; Element<Type>temp=list.Vector[i]; while (left<=Right){ int middle=(left+Right)/2; if (temp.getkey( )<list.Vector[middle].getkey( )) Right=middle-1; else left=middle+1; } for (int k=i-1; k>=left ; k--) list.Vector[k+1]=list.Vector[k];//向后移, O(n) list.Vector[left]=temp; }O(nlogn)
希尔排序没印象了,大概率没有
冒泡排序
简单
O(n^2)
快速排序
template <class Type> void QuickSort( datalist <Type>& list,const int left, const int right ) { if (left<right){ int pivotpos=partition (list, left, right); QuickSort(list, left, pivotpos-1); QuickSort(list, pivotpos+1, right); } } template <class Type> int partition(datalist<Type> &list,const int low, const int high) { int i=low, j=high; Element<Type>pivot=list.Vector[low];//一开始low的元素放在了pivot里面 while (i != j ){ while(list.Vector[j].getkey( )>pivot.getkey( ) && i<j) j--; if (i<j) {list.Vector[i]=list.Vector[j]; i++;} while(list.Vector[i].getkey( )<pivot.getkey( ) && i<j) i++; if (i<j) {list.Vector[j]=list.Vector[i]; j--;} }//找到左侧>=pivot且右侧<=pivot的位置,交换,直到左右相遇 list.Vector[i]=pivot ; return i; }
- 若 num[i] <= m 且 num[j] >= m,則 i++, j–
- 若 num[i] >m 且 num[j] < m,則 num[i], num[j] 交換並且 i++, j–
- 若 num[i] > m 而 num[j] >= m,則 j–
- 若 num[i] <= m 而 num[j] < m,則 i++
栈来存放: 1)存放什么:左部或右部的上、下界的下标。 2)栈要多大:O(log2n)~ O(n) <- 对应于有序情况
锦标赛排序应该不考
选择排序、堆排序(见上)
template <class Type> void SelectSort(datalist<Type> &list){ for ( int i=0; i<list.CurrentSize-1; i++) SelectExchange(list, i); } template <class Type> void SelectExchange( datalist<Type> &list, const int i){ int k=i; for ( int j=i+1; j<list.CurrentSize; j++) if (list.Vector[j].getkey( )<list.Vector[k].getkey( )) k=j; // 找到小于它的最靠后的节点 if ( k!=i) Swap(list.Vactor[i], list.Vector[k]); }O(n^2)
归并(重点)
public static void mergeSort( Comparable [ ] a ){ Comparable [ ] tmpArray = new Comparable[ a.length ]; mergeSort( a, tmpArray, 0, a.length – 1 ); } private static void mergeSort( Comparable [ ] a, Comparable [ ] tmpArray, int left, int right ){ if( left < right ){ int center = ( left + right ) / 2; mergeSort( a, tmparray, left, center ); mergeSort( a, tmpArray, center + 1, right ); merge( a, tmpArray, left, center + 1, right ); } } private static void merge( Comparable [ ] a, Comparable [ ] tmpArray, int leftPos, int rightPos, int rightEnd ){ int leftEnd = rightPos – 1; int tmpPos = leftPos; int numElements = rightEnd – leftPos + 1; while( leftPos <= leftEnd && rightPos <= rightEnd ) if( a[ leftPos ].compareTo( a[ rightPos ] ) <= 0 ) tmpArray[ tmpPos++ ] = a[ leftPos++ ]; else tmpArray[ tmpPos++ ] = a[ rightPos++ ]; while( leftPos <= leftEnd ) tmpArray[ tmpPos++ ] = a[ leftPos++ ]; while( rightpos <= rightEnd) tmpArray[ tmpPos++] = a[ rightpos++ ]; for( int i = 0; i < numElements; i++, rightEnd-- ) a[ rightEnd ] = tmpArray[ rightEnd ];//拷贝回a }O(nlogn)
题型
选择:单选(4分)
应该没有填空
问答题:看清楚问题有几个,详细
编程题:量较大,不能写伪代码,人工批,看清题目(不要乱改变量名)
期末占比80%,平时20%(看情况微调)